Theorema egregium
Gaussova Theorema Egregium (latinsky "Pozoruhodná veta") je významný výsledok diferenciálnej geometrie, ktorý dokázal Carl Friedrich Gauss. Veta sa týka zakrivenia plôch. Veta tvrdí, že zakrivenie možno určiť len meraním uhlov, vzdialeností a ich pomerov na povrchu. Nie je potrebné hovoriť o konkrétnom spôsobe, akým je povrch zasadený do okolitého trojrozmerného euklidovského priestoru. Inými slovami, Gaussova krivosť povrchu sa nezmení, ak povrch ohneme bez toho, aby sme ho natiahli.
Gauss prezentoval vetu týmto spôsobom (v preklade z latinčiny):
Z tohto dôvodu vzorec z predchádzajúceho článku vedie k pozoruhodnej vete. Ak zakrivenú plochu rozvinieme na akúkoľvek inú plochu, miera zakrivenia v každom bode zostane nezmenená.
Veta je "pozoruhodná", pretože východisková definícia Gaussovho zakrivenia priamo využíva polohu povrchu v priestore. Je teda dosť prekvapujúce, že výsledok nezávisí od jej osadenia napriek všetkým prekonaným ohybovým a krútivým deformáciám.
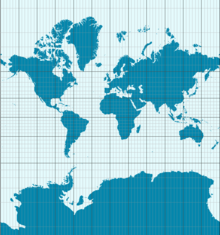
Dôsledkom Theorema Egregium je, že Zem sa nedá zobraziť na mape bez skreslenia. Mercatorova projekcia, znázornená na obrázku, zachováva uhly, ale mení plochu. Napríklad Antarktída je zobrazená oveľa väčšia, ako v skutočnosti je.
Otázky a odpovede
Otázka: Čo je Gaussova Theorema Egregium?
Odpoveď: Gaussova Theorema Egregium je významný výsledok diferenciálnej geometrie, ktorý sa týka zakrivenia plôch a ktorý dokázal Carl Friedrich Gauss.
Otázka: Ako sa dá určiť zakrivenie podľa Gaussovej Theorema Egregium?
Odpoveď: Podľa Gaussovej Theorema Egregium možno krivosť určiť len meraním uhlov, vzdialeností a ich pomerov na povrchu.
Otázka: Je na určenie zakrivenia potrebné hovoriť o konkrétnom spôsobe, akým je povrch zasadený do okolitého trojrozmerného euklidovského priestoru?
Odpoveď: Nie, na určenie zakrivenia podľa Gaussovej Theorema Egregium nie je potrebné hovoriť o konkrétnom spôsobe, akým je povrch zasadený do okolitého trojrozmerného euklidovského priestoru.
Otázka: Zmení sa Gaussova krivosť povrchu, ak povrch ohneme bez jeho natiahnutia?
Odpoveď: Nie, Gaussova krivosť povrchu sa nezmení, ak povrch ohneme bez jeho natiahnutia podľa Gaussovej Egregiovej tézy.
Otázka: Kto takto prezentoval túto vetu?
Odpoveď: Gauss predložil vetu týmto spôsobom.
Otázka: Čím je veta pozoruhodná?
Odpoveď: Veta je "pozoruhodná", pretože východisková definícia Gaussovej krivosti priamo využíva polohu plochy v priestore. Je teda dosť prekvapujúce, že výsledok nezávisí od jej osadenia napriek všetkým prekonaným ohybovým a krútivým deformáciám.
Otázka: Akým spôsobom Gauss prezentoval vetu?
Odpoveď: Gauss prezentoval vetu takým spôsobom, že ak sa zakrivená plocha rozvinie na ľubovoľnej inej ploche, miera zakrivenia v každom bode zostane nezmenená.
Prehľadať