Lineárna regresia
Lineárna regresia je spôsob, ako vysvetliť vzťah medzi závislou premennou a jednou alebo viacerými vysvetľujúcimi premennými pomocou priamky. Je to špeciálny prípad regresnej analýzy.
Lineárna regresia bola prvým typom regresnej analýzy, ktorý sa dôsledne skúmal. Je to preto, že modely, ktoré lineárne závisia od svojich neznámych parametrov, sa ľahšie fitujú ako modely, ktoré sú nelineárne závislé od svojich parametrov. Navyše sa ľahšie určujú štatistické vlastnosti výsledných odhadov.
Lineárna regresia má mnoho praktických využití. Väčšina aplikácií spadá do jednej z týchto dvoch širokých kategórií:
- Lineárnu regresiu možno použiť na priradenie predikčného modelu k súboru pozorovaných hodnôt (údajov). To je užitočné, ak je cieľom predikcia, prognóza alebo redukcia. Po vytvorení takéhoto modelu, ak je potom daná ďalšia hodnota X bez jej sprievodnej hodnoty y, možno fitovaný model použiť na predpovedanie hodnoty y.
- Vzhľadom na premennú y a niekoľko premenných X1, ..., Xp, ktoré môžu súvisieť s y, možno lineárnu regresnú analýzu použiť na kvantifikáciu sily vzťahu medzi y a Xj, na posúdenie, ktoré Xj vôbec nesúvisia s y, a na určenie, ktoré podmnožiny Xj obsahujú nadbytočné informácie o y.
Lineárne regresné modely sa snažia, aby vertikálna vzdialenosť medzi priamkou a dátovými bodmi (napr. rezíduá) bola čo najmenšia. Tento postup sa nazýva "prispôsobenie priamky údajom". Lineárne regresné modely sa často snažia minimalizovať súčet štvorcov rezíduí (najmenšie štvorce), ale existujú aj iné spôsoby prispôsobenia. Patrí medzi ne minimalizácia "nesúladu" v nejakej inej norme (ako pri regresii s najmenšími absolútnymi odchýlkami) alebo minimalizácia penalizovanej verzie stratovej funkcie najmenších štvorcov ako pri hrebeňovej regresii. Prístup najmenších štvorcov možno použiť aj na fitovanie modelov, ktoré nie sú lineárne. Ako bolo uvedené vyššie, pojmy "najmenšie štvorce" a "lineárny model" spolu úzko súvisia, ale nie sú to synonymá.
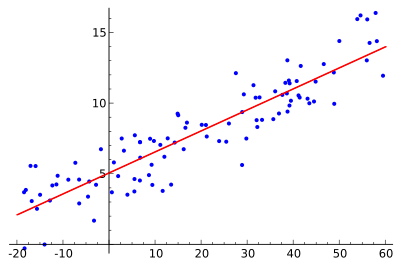
Cieľom je nájsť červenú krivku, modré body sú skutočné vzorky. Pri lineárnej regresii možno všetky body spojiť pomocou jedinej priamky. V tomto príklade sa používa jednoduchá lineárna regresia, pri ktorej sa minimalizuje štvorec vzdialenosti medzi červenou priamkou a každým bodom vzorky.
Použitie
Ekonomika
Lineárna regresia je hlavným analytickým nástrojom v ekonómii. Používa sa napríklad na odhad výdavkov na spotrebu, výdavkov na fixné investície, investícií do zásob, nákupov vývozu krajiny, výdavkov na dovoz, dopytu po držbe likvidných aktív, dopytu po práci a ponuky práce.
Otázky a odpovede
Otázka: Čo je to lineárna regresia?
Odpoveď: Lineárna regresia je spôsob, ako sa pomocou matematiky pozrieť na to, ako sa niečo zmení, keď sa zmenia iné veci. Používa závislú premennú a jednu alebo viac vysvetľujúcich premenných na vytvorenie priamky, známej ako "regresná priamka".
Otázka: Aké sú výhody lineárnej regresie?
Odpoveď: Modely, ktoré lineárne závisia od svojich neznámych parametrov, sa ľahšie prispôsobujú ako modely, ktoré sú nelineárne závislé od svojich parametrov. Okrem toho sa ľahšie určujú štatistické vlastnosti výsledných odhadov.
Otázka: Aké sú niektoré praktické spôsoby použitia lineárnej regresie?
Odpoveď: Lineárnu regresiu možno použiť na fitovanie predikčného modelu na pozorované hodnoty (údaje) s cieľom urobiť predpovede, prognózy alebo redukcie. Môže sa použiť aj na kvantifikáciu sily vzťahov medzi premennými a identifikáciu podmnožín údajov, ktoré obsahujú nadbytočné informácie o inej premennej.
Otázka: Ako sa lineárne regresné modely snažia minimalizovať chyby?
Odpoveď: Lineárne regresné modely sa snažia, aby vertikálna vzdialenosť medzi priamkou a dátovými bodmi (rezíduá) bola čo najmenšia. To sa dosahuje minimalizáciou buď súčtu štvorcov rezíduí (najmenšie štvorce), nedostatočnej zhody v nejakej inej norme (najmenšie absolútne odchýlky), alebo minimalizáciou penalizovanej verzie stratovej funkcie najmenších štvorcov (hrebeňová regresia).
Otázka: Je možné, aby lineárne regresné modely neboli založené na najmenších štvorcoch?
Odpoveď: Áno, je možné, aby lineárne regresné modely neboli založené na najmenších štvorcoch, ale aby namiesto toho používali metódy, ako je minimalizácia nedostatočnej zhody v nejakej inej norme (najmenšie absolútne odchýlky) alebo minimalizácia penalizovanej verzie stratovej funkcie najmenších štvorcov (ridge regresia).
Otázka: Sú "lineárny model" a "najmenšie štvorce" synonymá?
Odpoveď: Nie, nie sú to synonymá. Hoci sú úzko prepojené, "lineárny model" sa vzťahuje konkrétne na použitie priamky, zatiaľ čo "najmenšie štvorce" sa vzťahujú konkrétne na snahu minimalizovať chyby tým, že sa zabezpečí minimálna vertikálna vzdialenosť medzi priamkou a dátovými bodmi.
