Lavínový efekt
Lavínový efekt ("efekt zosuvu pôdy") je vlastnosť blokových šifier a algoritmov kryptografických hašovacích funkcií. V kryptografii je často žiadaná. Efekt hovorí, že sa musí zmeniť veľká časť výstupu, aj keď sa vstup zmení len málo. V dobrých blokových šifrách to znamená: Malá zmena kľúča alebo otvoreného textu by mala spôsobiť silnú zmenu šifrového textu.
To znamená, že malé zmeny sa môžu rýchlo šíriť, ak algoritmus používa iterácie. Každý bit výstupu teda závisí od každého bitu vstupu.
Termín lavínový efekt prvýkrát použil Horst Feistel (Feistel 1973). Neskôr bol tento pojem identifikovaný Shannonovou vlastnosťou zmätku.
Ak bloková šifra alebo kryptografická hašovacia funkcia nespĺňa lavínový efekt vo významnej miere, potom má slabú náhodnosť. Kryptoanalytik teda môže robiť prognózy o vstupe, ak mu je daný len výstup. To môže stačiť na čiastočné alebo úplné prelomenie (cracknutie) algoritmu.
Je to jeden z hlavných cieľov návrhu pri vytváraní silnej šifry alebo kryptografickej hašovacej funkcie. Snažia sa v nej vytvoriť dobrý lavínový efekt. Matematicky sa pri tom využíva efekt motýľa. Preto je väčšina blokových šifier súčinovými šiframi. To je tiež dôvod, prečo majú hašovacie funkcie veľké dátové bloky.
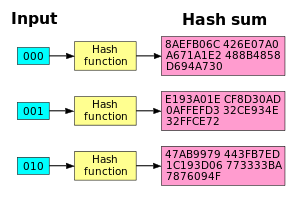
Hashovacia funkcia SHA1 má dobrý lavínový efekt. Keď sa zmení jediný bit, súčet hash sa úplne zmení.
Názov
Pôvod názvu sú zosuvy pôdy. Malý kameň môže spadnúť, spolu so snehom sa zosunúť a vytvoriť ničivý zosuv. Skala bola malá, ale mohla spôsobiť veľa skazy. To je to isté, čo robí tento efekt. Malá zmena na vstupe (skala) by mala zmeniť výstup (krajinu).
Prísne lavínové kritérium
Prísne lavínové kritérium (SAC; "silné zosuvné kritérium") je vlastnosť logických funkcií. Má význam pre kryptografiu. Je splnené, ak sa pri zmene jediného vstupného bitu zmenia všetky výstupné bity s pravdepodobnosťou 50 percent.
SAC bol postavený na konceptoch evolučnej úplnosti a lavínovitosti. Zaviedli ho Webster a Tavares v roku 1985. V súčasnosti je požiadavkou každého moderného kryptografického systému. Splnili ju napr. všetci finalisti súťaže AES.
Kritérium bitovej nezávislosti
Kritérium nezávislosti bitu (BIC; kritérium nezávislé od bitu) je kritérium. Platí: Keď sa zmení jeden vstupný bit (invertuje sa), dva výstupné bity by sa mali zmeniť nezávisle od seba. Toto platí pre všetky bity.
Nebolo by napr. vyhovujúce, keby sa jeden výstupný bit zmenil len vtedy, keď sa zmení aj druhý výstupný bit. Mohli by sa zmeniť len preto, že sa zmenil vstupný bit. V opačnom prípade by výstupné bity boli závislé jeden od druhého.
Súvisiace stránky
- Zmätok a difúzia
Otázky a odpovede
Otázka: Čo je to lavínový efekt?
Odpoveď: Lavínový efekt (známy aj ako "efekt lavíny") je vlastnosť blokových šifier a algoritmov kryptografických hašovacích funkcií, ktorá hovorí, že malá zmena kľúča alebo otvoreného textu by mala spôsobiť silnú zmenu šifrového textu.
Otázka: Kto ako prvý použil termín "lavínový efekt"?
Odpoveď: Termín lavínový efekt prvýkrát použil Horst Feistel v roku 1973.
Otázka: Ako súvisí so Shannonovou vlastnosťou zámeny?
Odpoveď: Pojem lavínový efekt bol identifikovaný Shannonovou vlastnosťou zmätočnosti, ktorá hovorí, že ak bloková šifra alebo kryptografická hašovacia funkcia nespĺňa tento stupeň vo významnej miere, potom má zlú náhodnosť a môže byť čiastočne alebo úplne prelomená (cracknutá).
Otázka: Aké sú niektoré ciele návrhu pri vytváraní silných šifier?
Odpoveď: Keď ľudia vytvárajú silné šifry, snažia sa do nich zabudovať dobrý lavínový efekt pomocou matematických princípov, ako je napríklad motýlí efekt. Preto je väčšina blokových šifier súčinovými šiframi a preto majú hašovacie funkcie veľké dátové bloky.
Otázka: Čo sa stane, ak algoritmus nespĺňa lavínový efekt?
Odpoveď: Ak algoritmus nespĺňa lavínový efekt vo významnej miere, potom má slabú náhodnosť a môže byť čiastočne alebo úplne prelomený (cracknutý) kryptoanalytikom, ktorý môže urobiť prognózu o vstupe len na základe daného výstupu.
Otázka: Prečo väčšina blokových šifier používa súčinové šifry?
Odpoveď: Väčšina blokových šifier používa súčinové šifry, pretože pomáhajú zabudovať do nich dobré avalančné efekty pomocou matematických princípov, ako je napríklad motýlí efekt.
Otázka: Prečo majú hašovacie funkcie veľké dátové bloky?
Odpoveď: Hašovacie funkcie majú veľké dátové bloky, pretože pomáhajú vytvárať dobré avalančné efekty pomocou matematických princípov, ako je napríklad efekt motýľa.
