Veta o štyroch farbách
Veta o štyroch farbách je matematická veta. Hovorí, že na ľubovoľnej rovinnej ploche s oblasťami (ľudia ich považujú za mapy) môžu byť oblasti vyfarbené najviac štyrmi farbami. Dve oblasti, ktoré majú spoločnú hranicu, nesmú dostať rovnakú farbu. Nazývajú sa susedné (vedľa seba), ak majú spoločnú úsečku hranice, nielen bod.
Bola to prvá veta, ktorú dokázal počítač, a to dôkazom vyčerpaním. Pri dôkaze vyčerpaním sa záver stanoví tak, že sa rozdelí na prípady a každý z nich sa dokazuje samostatne. Prípadov môže byť veľa. Napríklad prvý dôkaz vety o štyroch farbách bol dôkaz vyčerpaním s 1 936 prípadmi. Tento dôkaz bol kontroverzný, pretože väčšina prípadov bola overená počítačovým programom, nie ručne. Najkratší dnes známy dôkaz vety o štyroch farbách má stále viac ako 600 prípadov.
Aj keď bol tento problém prvýkrát prezentovaný ako problém vyfarbenia politických máp krajín, tvorcovia máp sa oň veľmi nezaujímajú. Podľa článku historika matematiky Kennetha Maya (Wilson 2002, 2) "mapy využívajúce len štyri farby sú zriedkavé a tie, ktoré ich využívajú, zvyčajne vyžadujú len tri. V knihách o kartografii a histórii tvorby máp sa vlastnosť štyroch farieb nespomína".
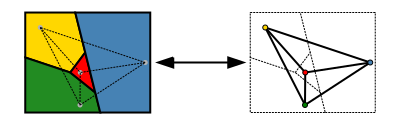
Mnohé jednoduchšie mapy možno vyfarbiť tromi farbami. Štvrtá farba je potrebná pri niektorých mapách, napríklad pri mapách, kde je jedna oblasť obklopená nepárnym počtom ďalších, ktoré sa navzájom dotýkajú v cykle. Jeden takýto príklad je uvedený na obrázku. Veta o piatich farbách hovorí, že na vyfarbenie mapy stačí päť farieb. Má krátky, elementárny dôkaz a bola dokázaná koncom 19. storočia. (Heawood 1890) Dokázať, že stačia štyri farby, sa ukázalo oveľa ťažšie. Od prvého vyhlásenia vety o štyroch farbách v roku 1852 sa objavilo mnoho falošných dôkazov a falošných protipríkladov.

Na vyfarbenie tejto mapy nestačia tri farby.

Príklad štvorfarebnej mapy
Presná formulácia problému
Intuitívne možno vetu o štyroch farbách vyjadriť takto: "Pri ľubovoľnom rozdelení roviny na susediace oblasti, ktoré sa nazýva mapa, možno tieto oblasti vyfarbiť najviac štyrmi farbami tak, aby žiadne dve susediace oblasti nemali rovnakú farbu. Aby bolo možné správne vyriešiť tento problém, je potrebné objasniť niektoré aspekty: Po prvé, všetky body, ktoré patria trom alebo viacerým krajinám, sa musia ignorovať. Po druhé, bizarné mapy s regiónmi s konečnou plochou a nekonečným obvodom môžu vyžadovať viac ako štyri farby.
Na účely tejto vety musí byť každá "krajina" jednoducho spojenou oblasťou alebo súvislou oblasťou. V reálnom svete to však nie je pravda: Aljaška ako súčasť Spojených štátov, Nachčivan ako súčasť Azerbajdžanu a Kaliningrad ako súčasť Ruska nie sú priľahlé. Keďže územie konkrétnej krajiny musí mať rovnakú farbu, štyri farby nemusia stačiť. Uvažujte napríklad o zjednodušenej mape, ako je zobrazená naľavo: Na tejto mape patria dva regióny označené písmenom A k tej istej krajine a musia mať rovnakú farbu. Táto mapa potom vyžaduje päť farieb, pretože dva regióny A spolu susedia so štyrmi ďalšími regiónmi, z ktorých každý susedí so všetkými ostatnými. Ak by mal región A len tri regióny, bolo by potrebných šesť alebo viac farieb. Týmto spôsobom je možné vytvoriť mapy, ktoré potrebujú ľubovoľne vysoký počet farieb. Podobná konštrukcia platí aj v prípade, ak sa pre všetky vodné plochy použije jediná farba, ako je to obvyklé na skutočných mapách.
Jednoduchšie formulovateľná verzia vety využíva teóriu grafov. Množinu regiónov mapy možno abstraktnejšie reprezentovať ako neorientovaný graf, ktorý má vrchol pre každý región a hranu pre každú dvojicu regiónov, ktoré majú spoločnú hraničnú úsečku. Tento graf je rovinný: možno ho nakresliť v rovine bez kríženia tak, že každý vrchol sa umiestni na ľubovoľne zvolené miesto v rámci regiónu, ktorému zodpovedá, a hrany sa nakreslia ako krivky, ktoré vedú bez kríženia v rámci každého regiónu z miesta vrcholu do každého spoločného hraničného bodu regiónu. Naopak, týmto spôsobom možno z mapy vytvoriť akýkoľvek rovinný graf. V grafovo-teoretickej terminológii veta o štyroch farbách hovorí, že vrcholy každého planárneho grafu možno vyfarbiť najviac štyrmi farbami tak, aby žiadne dva susedné vrcholy nemali rovnakú farbu, alebo skrátene "každý planárny graf je štvorfarebný" (Thomas 1998, s. 849; Wilson 2002).

Príklad mapy Azerbajdžanu s nesúvislými regiónmi

Túto mapu nemožno vyfarbiť štyrmi farbami
História
Ako prvý pomenoval tento problém Francis Guthrie v roku 1852. V tom čase bol študentom práva v Anglicku. Zistil, že na vyfarbenie mapy anglických grófstiev potrebuje aspoň štyri farby. Augustus de Morgan prvýkrát diskutoval o tomto probléme v liste, ktorý napísal Rowanovi Hamlitonovi v auguste 1852. V liste sa de Morgan pýta, či štyri farby naozaj stačia na vyfarbenie mapy tak, aby krajiny, ktoré sú vedľa seba, dostali rôzne farby.
Anglický matematik Arthur Cayley predstavil tento problém matematickej spoločnosti v Londýne v roku 1878. O rok Alfred Kempe našiel niečo, čo vyzeralo ako dôkaz problému. O jedenásť rokov neskôr, v roku 1890, Percy Heawood ukázal, že Alfredov dôkaz bol nesprávny. Peter Guthrie Tait predložil ďalší pokus o dôkaz v roku 1880. Trvalo jedenásť rokov, kým sa ukázalo, že ani Taitov dôkaz nefunguje. V roku 1891 to mohol dokázať Julius Petersen. Keď falzifikoval Cayleyho dôkaz, Kempe ukázal aj dôkaz pre problém, ktorý nazval Veta o piatich farbách. Veta hovorí, že každú takúto mapu možno vyfarbiť najviac piatimi farbami. Existujú dve obmedzenia: Po prvé, každá krajina je súvislá, neexistujú žiadne exklávy. Druhé obmedzenie spočíva v tom, že krajiny musia mať spoločnú hranicu; ak sa dotýkajú len v jednom bode, môžu byť vyfarbené rovnakou farbou. Hoci Kempeho dôkaz bol nesprávny, použil niektoré myšlienky, ktoré neskôr umožnili správny dôkaz.
V 60. a 70. rokoch 20. storočia Heinrich Heesch vytvoril prvý náčrt počítačového dôkazu. Kenneth Appel a Wolfgang Haken tento náčrt v roku 1976 vylepšili (Robertson et al. 1996). Podarilo sa im znížiť počet prípadov, ktoré by bolo potrebné otestovať, na 1936; neskôr vznikla verzia, ktorá sa spoliehala na testovanie len 1476 prípadov. Každý prípad bolo potrebné otestovať pomocou počítača (Appel a Haken 1977).
V roku 1996 Neil Robertson, Daniel Sanders, Paul Seymour a Robin Thomas túto metódu vylepšili a počet testovaných prípadov znížili na 663. Aj v tomto prípade bolo potrebné každý prípad testovať pomocou počítača.
V roku 2005 Georges Gonthier a Benjamin Werner vypracovali formálny dôkaz. Išlo o zlepšenie, pretože po prvýkrát umožnilo použiť softvér na dokazovanie tvrdení. Použitý softvér sa nazýva Coq.
Veta o štyroch farbách je prvý veľký matematický problém, ktorý bol dokázaný pomocou počítača. Keďže dôkaz nemôže vykonať človek, niektorí matematici ho neuznali za správny. Na overenie dôkazu je potrebné spoliehať sa na správne fungujúci softvér a hardvér na overenie dôkazu. Keďže dôkaz bol vykonaný pomocou počítača, nie je ani veľmi elegantný.
Pokusy, ktoré sa ukázali ako nesprávne
Veta o štyroch farbách je známa tým, že počas svojej dlhej histórie prilákala veľké množstvo falošných dôkazov a nedokazov. Denník The New York Times najprv odmietol informovať o Appelovom-Hakenovom dôkaze. Noviny tak urobili v rámci svojej politiky; obávali sa, že dôkaz sa ukáže ako nepravdivý rovnako ako tie predchádzajúce (Wilson 2002, s. 209). Niektoré dôkazy trvali dlho, kým sa ich podarilo sfalšovať: V prípade Kempeho a Taitových dôkazov ich falšovanie trvalo viac ako desať rokov.
Najjednoduchšie protipríklady sa vo všeobecnosti snažia vytvoriť jednu oblasť, ktorá sa dotýka všetkých ostatných. To núti zvyšné oblasti vyfarbiť len tromi farbami. Keďže platí veta o štyroch farbách, je to vždy možné; pretože sa však osoba kresliaca mapu sústredí na jeden veľký región, nevšimne si, že zvyšné regióny môžu byť v skutočnosti vyfarbené tromi farbami.
Tento trik sa dá zovšeobecniť: Ak sú farby niektorých oblastí na mape vybrané vopred, nie je možné vyfarbiť zvyšné oblasti tak, aby sa celkovo použili len štyri farby. Niekoho, kto overuje protipríklad, nemusí napadnúť, že môže byť potrebné zmeniť farbu týchto regiónov. Protipríklad tak bude vyzerať platný, aj keď nie je.
Jedným z efektov, ktoré sú základom tejto bežnej mylnej predstavy, je možno skutočnosť, že farebné obmedzenie nie je tranzitívne: región musí byť zafarbený inak len v porovnaní s regiónmi, ktorých sa priamo dotýka, a nie v porovnaní s regiónmi, ktorých sa dotýka. Ak by toto obmedzenie platilo, rovinné grafy by vyžadovali ľubovoľne veľký počet farieb.
Iné falošné dôkazy porušujú predpoklady vety neočakávaným spôsobom, napríklad použitím oblasti, ktorá má viacero nespojitých častí, alebo nedovolením, aby sa oblasti rovnakej farby dotýkali v bode.
Farbenie politických máp
V skutočnom živote má mnoho krajín exklávy alebo kolónie. Keďže patria ku krajine, musia byť vyfarbené rovnakou farbou ako materská krajina. To znamená, že na vyfarbenie takejto mapy sú zvyčajne potrebné viac ako štyri farby. Keď matematici hovoria o grafe spojenom s touto úlohou, hovoria, že nie je rovinný. Aj keď je ľahké skontrolovať, či je graf planárny, nájsť najmenší počet farieb potrebných na jeho vyfarbenie je veľmi ťažké. Je NP-úplný, čo je jeden z najťažších problémov, ktoré existujú. Najmenší počet farieb potrebných na vyfarbenie grafu je známy ako jeho chromatické číslo. Mnohé problémy, ktoré sa vyskytujú pri snahe vyriešiť vetu o štyroch farbách, súvisia s diskrétnou matematikou. Z tohto dôvodu sa často používajú metódy z algebraickej topológie.
Rozšírenie na "neploché" mapy
Veta o štyroch farbách vyžaduje, aby "mapa" bola na rovnej ploche, ktorú matematici nazývajú rovina. V roku 1890 Percy John Heawood vytvoril to, čo sa dnes nazýva Heawoodova domnienka: V nej sa kladie rovnaká otázka ako v vete o štyroch farbách, ale pre akýkoľvek topologický objekt. Ako príklad možno uviesť torus, ktorý možno zafarbiť najviac siedmimi farbami. Heawoodova domnienka dáva vzorec, ktorý funguje pre všetky takéto objekty okrem Kleinovej fľaše.
Otázky a odpovede
Otázka: Čo je to veta o štyroch farbách?
Odpoveď: Veta o štyroch farbách je matematická veta, ktorá hovorí, že na ľubovoľnej rovinnej ploche s oblasťami môžu byť oblasti vyfarbené najviac štyrmi farbami. Susediace oblasti nesmú mať rovnakú farbu.
Otázka: Ako vznikol prvý dôkaz vety o štyroch farbách?
Odpoveď: Prvý dôkaz vety o štyroch farbách bol dôkaz vyčerpaním s 1 936 prípadmi. To znamená, že bola stanovená rozdelením na prípady a dokazovaním každého z nich osobitne.
Otázka: Zaujímajú sa kartografi o tento problém?
Odpoveď: Nie, kartografov tento problém veľmi nezaujíma, pretože mapy využívajúce iba štyri farby sú zriedkavé a zvyčajne vyžadujú iba tri farby. V knihách o kartografii a histórii tvorby máp sa vlastnosť štyroch farieb nespomína.
Otázka: Čo je to veta o piatich farbách?
Odpoveď: Veta o piatich farbách hovorí, že na vyfarbenie mapy stačí päť farieb, a má krátky, elementárny dôkaz, ktorý bol dokázaný koncom 19. storočia.
Otázka: Aké ťažké bolo dokázať, že na vyfarbenie mapy sú potrebné len 4 farby?
Odpoveď: Dokázať, že na vyfarbenie máp sú potrebné len 4 farby, sa ukázalo byť oveľa ťažšie, ako sa očakávalo, pretože od jej prvého vyhlásenia v roku 1852 sa objavilo mnoho falošných dôkazov a falošných protipríkladov.
Otázka: Existuje príklad mapy, na ktorej správne vyfarbenie všetkých regiónov by bolo potrebných 5 alebo viac farieb?
Odpoveď: Áno, jedným z takýchto príkladov je situácia, keď je jeden región obklopený nepárnym počtom ďalších, ktoré sa navzájom dotýkajú v cykle - v tomto prípade môže byť na správne vyfarbenie všetkých regiónov potrebných 5 alebo viac farieb.
Prehľadať

