Fraktál

Príklady

Existuje mnoho typov fraktálov, ktoré sú vytvorené najrôznejšími spôsobmi. Jedným z príkladov je Sierpinského trojuholník, kde sa vo vnútri veľkého trojuholníka nachádza nekonečné množstvo malých trojuholníkov. Ďalším príkladom je Mandelbrotova množina, pomenovaná podľa Benoîta Mandelbrota. Sierpinksiho trojuholník je skonštruovaný pomocou obrazcov, ale Mandelbrotova množina je založená na rovnici.

V prírode je tiež mnoho prírodných príkladov fraktálov vrátane stromov, snehových vločiek, niektorých druhov zeleniny a pobrežných línií.

Kochova krivka

Kochova krivka je jednoduchým príkladom fraktálu. Najprv začnite s časťou priamky - tzv. úsečkou. Priamku rozrežte na 3 rovnako veľké časti. Zbavte sa stredných z týchto kúskov a vložte do nich vrchnú časť trojuholníka so stranami, ktoré sú rovnako dlhé ako kúsok, ktorý treba vyrezať. Teraz máme 4 úsečky, ktoré sa na koncoch dotýkajú. To, čo sme práve urobili s prvou úsečkou, môžeme teraz urobiť s každým zo 4 kúskov. To isté teraz môžeme opakovať so všetkými bitmi, ktoré nám nakoniec vzniknú. Teraz to budeme robiť donekonečna a pozrieme sa, čo nám nakoniec vznikne.

Dĺžka Kochovej krivky je nekonečno a plocha Kochovej krivky je nula. To je dosť zvláštne. Úsečka (s rozmerom 1) môže mať dĺžku 1, ale jej plocha je 0. Štvorec s dĺžkou 1 a šírkou 1 (s rozmerom 2) bude mať plochu 1 a dĺžku nekonečno.

Rozmer podobnosti

Takže Kochova krivka sa zdá byť väčšia ako niečo s rozmerom 1 a menšia ako niečo s rozmerom 2. Zmyslom podobnostnej dimenzie je poskytnúť dimenziu, ktorá poskytuje lepšiu predstavu o dĺžke alebo ploche fraktálov. Takže pre Kochovu krivku chceme rozmer medzi 1 a 2.

Kochovu krivku možno rozrezať na štyri časti, z ktorých každá má 1 3 {\displaystyle {\frac {1}{3}}} veľkosti originálu. Počet častí, na ktoré sa dá fraktál rozrezať, nazývame N {\displaystyle N} , a rozdiel veľkostí nazývame B {\displaystyle B} . Tieto údaje dosadíme do rovnice:

log N - log B {\displaystyle {\frac {\log N}{-log B}}

Kde log {\displaystyle \log } je logaritmus čísla. Toto číslo je Hausdorffova dimenzia fraktálu. V prípade Kochovej krivky je to log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1,2619... } ako sme chceli.

Kochova krivka je jedným z najjednoduchších fraktálnych útvarov, a preto je ľahké určiť jej rozmer. Jej dimenzia podobnosti a Hausdorffova dimenzia sú rovnaké. Pre zložitejšie fraktály to neplatí.

Kochova snehová vločka

Kochova snehová vločka (alebo Kochova hviezda) je rovnaká ako Kochova krivka, len namiesto úsečky začína rovnostranným trojuholníkom.

Ako vytvoriť Kochovu krivku

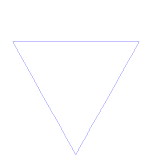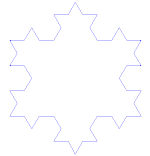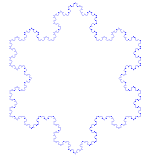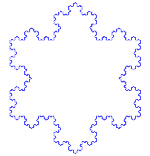
Používa

Fraktály majú mnoho aplikácií, napr. v biológii (pľúca, obličky, variabilita srdcovej frekvencie atď...), pri zemetraseniach, vo financiách, kde súvisia s tzv. ťažkými chvostovými rozdeleniami, a vo fyzike. To naznačuje, že fraktály by sa mali študovať, aby sme pochopili, prečo sú fraktály v prírode také časté.

Niektoré fraktály existujú len z umeleckých dôvodov, iné sú však veľmi užitočné. Fraktály sú veľmi efektívne tvary pre rádiové antény a používajú sa v počítačových čipoch na efektívne prepojenie všetkých komponentov. Aj pobrežné čiary možno považovať za fraktály.