Logaritmus

História

Logaritmy boli prvýkrát použité v Indii v 2. storočí pred naším letopočtom. V novoveku logaritmy ako prvý použil nemecký matematik Michael Stifel (okolo roku 1487 - 1567). V roku 1544 zapísal tieto rovnice: q m q n = q m + n {\displaystyle q^{m}q^{n}=q^{m+n}} a q m q n = q m - n {\displaystyle {\tfrac {q^{m}}{q^{n}}}=q^{m-n}} Toto je základ pre pochopenie logaritmov. Pre Stifela m {\displaystyle m} a n {\displaystyle n} museli byť celé čísla. John Napier (1550-1617) nechcel toto obmedzenie a chcel rozsah pre exponenty.

Podľa Napiera logaritmy vyjadrujú pomery: a {\displaystyle a} má rovnaký pomer k b {\displaystyle b} , ako c {\displaystyle c} k d {\displaystyle d}, ak sa zhoduje rozdiel ich logaritmov. Matematicky: log ( a ) - log ( b ) = log ( c ) - log ( d ) {\displaystyle \log(a)-\log(b)=\log(c)-\log(d)} . Najprv sa používal základ e (aj keď toto číslo ešte nebolo pomenované). Henry Briggs navrhol používať ako základ pre logaritmy číslo 10. Takéto logaritmy sú veľmi užitočné v astronómii.

John Napier pracoval na logaritmoch

Vzťah s exponenciálnymi funkciami

Logaritmus hovorí, aký exponent (alebo mocnina) je potrebný na vytvorenie určitého čísla, takže logaritmy sú inverzné (opačné) k exponenciám.

Tak ako exponenciálna funkcia má tri časti, aj logaritmus má tri časti. Tri časti logaritmu sú základ, argument a odpoveď (nazývaná aj mocnina).

Ide o exponenciálnu funkciu:

2 3 = 8 {\displaystyle 2^{3}=8\ }

V tejto funkcii je základom 2, argumentom je 3 a odpoveďou je 8.

Táto exponenciálna funkcia má inverznú hodnotu, svoj logaritmus:

log 2 ( 8 ) = 3 {\displaystyle \log _{2}(8)=3\ }

V tomto logaritme je základ 2, argument 8 a odpoveď 3.

Rozdiel oproti koreňom

Sčítanie má jednu inverznú operáciu: odčítanie. Aj násobenie má jednu inverznú operáciu: delenie. Preto môže byť ťažké pochopiť, prečo má exponenciála vlastne dve inverzné operácie: Prečo potrebujeme logaritmus, keď už existuje koreň? Je to tak preto, lebo exponenciácia nie je komutatívna.

Nasledujúci príklad to ilustruje:

• Ak máte x+2=3, môžete pomocou odčítania zistiť, že x=3-2. To isté platí, ak máte 2+x=3: tiež dostanete x=3-2. Je to preto, že x+2 je to isté ako 2+x.
• Ak máte x - 2=3, potom môžete pomocou delenia zistiť, že x= 3 2 {\textstyle {\frac {3}{2}}} . To isté platí, ak máte 2 - x=3: tiež dostanete x= 3 2 {\textstyle {\frac {3}{2}}} . Je to preto, že x - 2 je to isté ako 2 - x.
• Ak máte x²=3, potom na zistenie x použijete (druhú) odmocninu: Dostanete výsledok x = 3 {\textstyle {\sqrt {3}}} . Ak však máte 2^x =3, potom nemôžete použiť koreň na zistenie x. Na zistenie x musíte skôr použiť (dvojkový) logaritmus: Dostanete výsledok x=log₂(3).
  Je to preto, že 2 ^xzvyčajne nie je rovnaké ako x ²(napríklad 2 ⁵=32, ale 5²=25).

Používa

Logaritmy môžu uľahčiť násobenie a delenie veľkých čísel, pretože sčítanie logaritmov je rovnaké ako násobenie a odčítanie logaritmov je rovnaké ako delenie.

Predtým, ako sa kalkulačky stali populárnymi a bežnými, ľudia používali na násobenie a delenie logaritmické tabuľky v knihách. Rovnaké informácie v logaritmickej tabuľke boli k dispozícii na posuvnom pravidle, nástroji s napísanými logaritmami.

• Logaritmické špirály sú v prírode bežné. Príkladom je schránka nautilu alebo usporiadanie semien na slnečnici.
• V chémii je záporná hodnota logaritmu aktivity hydroniových iónov (H₃O ⁺, forma H vo ⁺vode) známa ako pH. Aktivita hydróniových iónov v neutrálnej vode je 10 ⁻⁷mol/l pri 25 °C, teda pH 7. (Je to dôsledok rovnovážnej konštanty, súčinu koncentrácie hydróniových iónov a hydroxylových iónov vo vodných roztokoch, ktorá je 10 ⁻¹⁴M ².)
• Richterova stupnica meria intenzitu zemetrasenia na logaritmickej stupnici so základom 10.
• V astronómii meria zdanlivá magnitúda jasnosť hviezd logaritmicky, pretože oko tiež reaguje na jas logaritmicky.
• Hudobné intervaly sa merajú logaritmicky ako poltóny. Interval medzi dvoma tónmi v poltónoch je logaritmus základu 2^1/12 pomeru frekvencií (alebo ekvivalentne 12-násobok logaritmu základu 2). Zlomkové poltóny sa používajú pri nerovnakých temperáciách. Najmä na meranie odchýlok od rovnomerne temperovanej stupnice sa intervaly vyjadrujú aj v centoch (stotinách rovnomerne temperovaného poltónu). Interval medzi dvoma tónmi v centoch je logaritmus základu 2^1/1200 pomeru frekvencií (alebo 1200 krát logaritmus základu 2). V MIDI sa noty číslujú na poltónovej stupnici (logaritmická absolútna nominálna výška so stredným C na 60). Na mikroladenie do iných ladiacich systémov sa definuje logaritmická stupnica, ktorá kompatibilným spôsobom vypĺňa rozsahy medzi poltónmi rovnomerne temperovanej stupnice. Táto stupnica zodpovedá číslam nôt pre celé poltóny. (pozri mikroladenie v MIDI).

Bežné logaritmy

Logaritmy do základu 10 sa nazývajú obyčajné logaritmy. Zvyčajne sa zapisujú bez základu. Napríklad:

log ( 100 ) = 2 {\displaystyle \log(100)=2\ }

To znamená:

10 2 = 100 {\displaystyle 10^{2}=100\ }

Prirodzené logaritmy

Logaritmy do základu e sa nazývajú prirodzené logaritmy. Číslo e je takmer 2,71828 a nazýva sa aj Eulerova konštanta podľa matematika Leonharda Eulera.

Prirodzené logaritmy môžu mať symboly log e ( x ) {\displaystyle \log _{e}(x)\,} alebo ln ( x ) {\displaystyle \ln(x)\,}

Niektorí autori uprednostňujú používanie prirodzených logaritmov ako log ( x ) {\displaystyle \log(x)}, ale zvyčajne to uvádzajú na úvodných stranách.

Spoločné základy pre logaritmy

základňa	skratka	Komentáre
2	ld {\displaystyle \operatorname {ld} }	Veľmi časté v informatike (binárne)
e	ln {\displaystyle \ln } alebo jednoducho log {\displaystyle \log }	Základom je Eulerova konštanta e. Je to najbežnejší logaritmus používaný v čistej matematike.
10	log 10 {\displaystyle \log _{10}} alebo log {\displaystyle \log } (niekedy tiež písané ako lg {\displaystyle \lg } )	Používa sa v niektorých vedách, ako je chémia a biológia.
ľubovoľné číslo, n	log n {\displaystyle \log _{n}}	Toto je všeobecný spôsob zápisu logaritmov

Vlastnosti logaritmov

Logaritmy majú mnoho vlastností. Napríklad:

Vlastnosti z definície logaritmu

Táto vlastnosť vyplýva priamo z definície logaritmu:

log n ( n a ) = a {\displaystyle \log _{n}(n^{a})=a} Napríklad

log 2 ( 2 3 ) = 3 {\displaystyle \log _{2}(2^{3})=3} a

log 2 ( 1 2 ) = - 1 {\displaystyle \log _{2}{\bigg (}{\frac {1}{2}}{\bigg )}=-1} pretože 1 2 = 2 - 1 {\displaystyle {\frac {1}{2}}=2^{-1}} .

Logaritmus na základ b čísla a je rovnaký ako logaritmus čísla a vydelený logaritmom čísla b. To znamená,

log b ( a ) = log ( a ) log ( b ) {\displaystyle \log _{b}(a)={\frac {\log(a)}{\log(b)}}}

Nech je napríklad a 6 a b 2. Pomocou kalkulačiek môžeme ukázať, že je to pravda alebo aspoň veľmi blízko:

log 2 ( 6 ) = log ( 6 ) log ( 2 ) {\displaystyle \log _{2}(6)={\frac {\log(6)}{\log(2)}}}

log 2 ( 6 ) ≈ 2,584962 {\displaystyle \log _{2}(6)\aprox 2,584962}

2,584962 ≈ 0,778151 0,301029 ≈ 2,584970 {\displaystyle 2,584962\approx {\frac {0,778151}{0,301029}}\approx 2,584970}

Naše výsledky mali malú chybu, ale tá bola spôsobená zaokrúhľovaním čísel.

Keďže je ťažké predstaviť si prirodzený logaritmus, zistíme, že z hľadiska logaritmu so základom desať:

ln ( x ) = log ( x ) log ( e ) ≈ log ( x ) 0,434294 {\displaystyle \ln(x)={\frac {\log(x)}{\log(e)}}\approx {\frac {\log(x)}{0,434294}}} Kde 0,434294 je aproximácia logaritmu e.

 

Operácie v rámci argumentov logaritmu

Logaritmy, ktoré sa násobia vnútri svojho argumentu, možno zmeniť takto:

log ( a b ) = log ( a ) + log ( b ) {\displaystyle \log(ab)=\log(a)+\log(b)}

Napríklad,

log ( 1000 ) = log ( 10 ⋅ 10 ⋅ 10 ) = log ( 10 ) + log ( 10 ) + log ( 10 ) = 1 + 1 + 1 = 3 {\displaystyle \log(1000)=\log(10\cdot 10\cdot 10)=\log(10)+\log(10)+\log(10)=1+1+1=3}

To isté platí aj pre delenie, ale namiesto sčítania sa používa odčítanie, pretože je to inverzná operácia k násobeniu:

log ( a b ) = log ( a ) - log ( b ) {\displaystyle \log {\bigg (}{\frac {a}{b}}{\bigg )}=\log(a)-\log(b)}

Logaritmické tabuľky, posuvné pravidlá a historické aplikácie

Pred elektronickými počítačmi používali vedci logaritmy každý deň. Logaritmy pomáhali vedcom a inžinierom v mnohých oblastiach, napríklad v astronómii.

Pred počítačmi bola dôležitým nástrojom tabuľka logaritmov. V roku 1617 Henry Briggs vytlačil prvú logaritmickú tabuľku. Bolo to krátko po Napierovom základnom vynáleze. Neskôr ľudia vytvárali tabuľky s väčším rozsahom a presnosťou. Tieto tabuľky uvádzali hodnoty log_b(x) a b ^xpre ľubovoľné číslo x v určitom rozsahu, s určitou presnosťou, pre určitý základ b (zvyčajne b = 10). Napríklad Briggsova prvá tabuľka obsahovala obyčajné logaritmy všetkých celých čísel v rozsahu 1-1000 s presnosťou 8 číslic. Keďže funkcia f(x) = b ^xje inverznou funkciou log _b(x), nazýva sa antilogaritmus. Ľudia tieto tabuľky používali na násobenie a delenie čísel. Používateľ napríklad vyhľadal v tabuľke logaritmus pre každé z dvoch kladných čísel. Sčítaním čísel z tabuľky by získal logaritmus súčinu. Funkcia antilogaritmu v tabuľke by potom našla súčin na základe jeho logaritmu.

Pri manuálnych výpočtoch, ktoré vyžadujú presnosť, je vykonanie vyhľadania dvoch logaritmov, výpočet ich súčtu alebo rozdielu a vyhľadanie antilogaritmu oveľa rýchlejšie ako vykonanie násobenia predchádzajúcimi spôsobmi.

Mnohé logaritmické tabuľky uvádzajú logaritmy tak, že samostatne uvádzajú charakteristiku a mantisu x, t. j. celočíselnú časť a zlomkovú časť log ₁₀(x). Charakteristika 10 - x je jedna plus charakteristika x a ich signifikancia je rovnaká. Tým sa rozširuje rozsah logaritmických tabuliek: ak je daná tabuľka s log ₁₀(x) pre všetky celé čísla x od 1 do 1000, logaritmus čísla 3542 sa aproximuje takto

log 10 ( 3542 ) = log 10 ( 10 ⋅ 354,2 ) = 1 + log 10 ( 354,2 ) ≈ 1 + log 10 ( 354 ) . {\displaystyle \log _{10}(3542)=\log _{10}(10\cdot 354,2)=1+\log _{10}(354,2)\aprox 1+\log _{10}(354).\,}

Ďalšou dôležitou aplikáciou bolo posuvné pravidlo, dvojica logaritmicky rozdelených stupníc, ktoré sa používali na výpočty, ako je znázornené na tomto obrázku:

Čísla sú vyznačené na posuvných stupniciach vo vzdialenostiach úmerných rozdielom ich logaritmov. Posúvanie hornej stupnice sa rovná mechanickému sčítaniu logaritmov. Napríklad pripočítaním vzdialenosti od 1 do 2 na spodnej stupnici k vzdialenosti od 1 do 3 na hornej stupnici sa získa súčin 6, ktorý sa odčíta na spodnej časti. Mnohí inžinieri a vedci používali posuvné pravidlá až do 70. rokov 20. storočia. Vedci môžu pracovať rýchlejšie pomocou posuvného pravidla ako pomocou logaritmickej tabuľky.

Schematické znázornenie posuvného meradla. Od čísla 2 na spodnej stupnici pripočítajte vzdialenosť k číslu 3 na hornej stupnici, aby ste získali súčin 6. Pravítko funguje, pretože je označené tak, že vzdialenosť od 1 k x je úmerná logaritmu x.


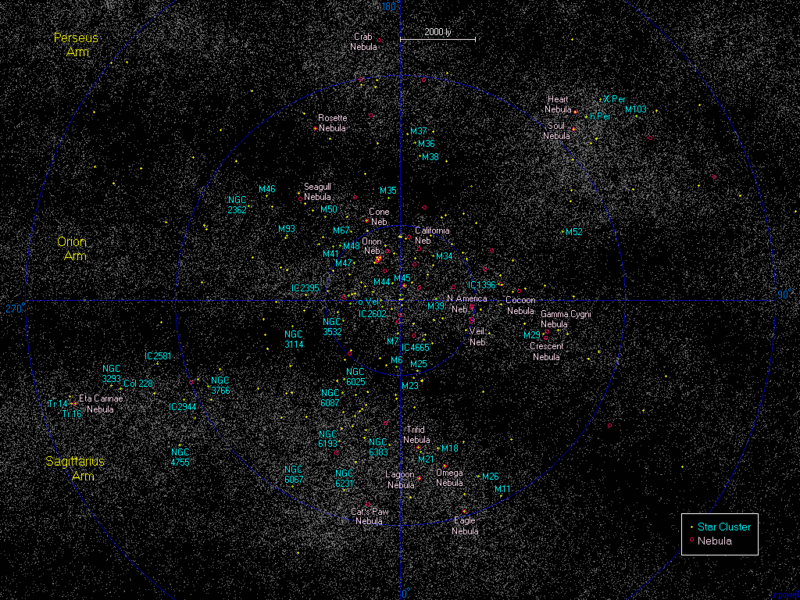
Najbližšie hmloviny a hviezdokopy (klikateľná mapa)