Zlatý rez (zlatý pomer): definícia, vzorec a vlastnosti φ
Objavte zlatý rez (φ): definícia, vzorec φ=(1+√5)/2, vlastnosti, história a praktické použitia v umení, architektúre a prírode.
Pri jednom čísle a a inom menšom čísle b podiel týchto dvoch čísel zistí ich delením. Ich pomer je a/b. Ďalší pomer sa zistí tak, že sa obe čísla sčítajú a+b a vydelia väčším číslom a. Nový pomer je (a+b)/a. Ak sa tieto dva pomery rovnajú rovnakému číslu, potom sa toto číslo nazýva zlatý rez. Grécke písmeno φ {\displaystyle \varphi } 
(fí) sa bežne používa ako označenie pre zlatý rez.
Napríklad, ak b = 1 a a/b = φ {\displaystyle \varphi } , potom a = φ {\displaystyle \varphi } . Druhý pomer (a+b)/a je potom ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } 
. Keďže tieto dva pomery sú rovnaké, platí:
φ = (φ + 1)/φ
Riešením tejto rovnice dostaneme známy uzavretý tvar
φ = (1 + √5) / 2
√5 
je kladné číslo, ktoré po vynásobení sebou samým dáva 5, teda √5 × √5 = 5 
.
Zlatý rez je iracionálne číslo. Jeho desatinné vyjadrenie nezačne a nikdy sa nekončí ani neopakuje v periodickom zlomku; začína približne takto: 1,6180339887... Dôležitou vlastnosťou φ je samopodobnosť: od čísla φ môžeme odčítať 1 alebo ním môžeme vydeliť 1 a výsledok má rovnaký tvar. Konkrétne platí
- φ^2 = φ + 1
- 1/φ = φ − 1
Algebraické vlastnosti
φ je algebraické číslo stupňa 2: je to riešenie kvadratickej rovnice
x² − x − 1 = 0.
Z tejto rovnice vyplýva φ = (1 + √5)/2 a druhé riešenie (konjugát) je ψ = (1 − √5)/2 ≈ −0,6180339887.... Medzi ďalšie užitočné identity patrí pre prirodzené n
- φ^n = F_n·φ + F_{n−1}, kde F_n sú Fibonacciho čísla
- lim (F_{n+1}/F_n) = φ (pomery susedných Fibonacciho čísel konvergujú k φ)
- φ má najjednoduchší nekonečný zretezený zlomok: φ = [1; 1, 1, 1, ...]
Geometrické a vizuálne vlastnosti
Zlatý rez sa často definuje geometricky: ak je segment rozdelený na dve časti tak, že pomer celej dĺžky k väčšej časti je rovnaký ako pomer väčšej časti k menšej, tento pomer je φ. Praktické dôsledky tejto vlastnosti sú zrejmé pri zostavovaní zlatého obdĺžnika (strany v pomere φ), ktorý možno ďalej rozdeľovať a dostávať samopodobné tvary (samopodobnosť súvisí s celotnými mocninami φ).
Použitie a výskyt
Zlatý rez sa vyskytuje v matematike (napr. v pravidelných päťuholníkoch a pentagónoch), v prírode (odvetvia rastlín, špirály lastúr), v umení a architektúre (kompozície, pomery rozmerov). V mnohých prípadoch poskytuje esteticky príjemné proporcie, hoci ich využitie v histórii umenia býva čiastočne idealizované.
Krátke zhrnutie
- Definícia: φ je pomer, pri ktorom (a+b)/a = a/b.
- Vzorec: φ = (1 + √5)/2 ≈ 1,6180339887...
- Algebraicky: φ² = φ + 1, 1/φ = φ − 1, min. polynóm x² − x − 1 = 0.
- Prepojenie s Fibonacciho postupnosťou a zretezenými zlomkami.
Zlatý obdĺžnik
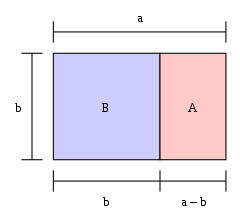
Ak sa dĺžka obdĺžnika delená jeho šírkou rovná zlatému rezu, ide o "zlatý obdĺžnik". Ak sa z jedného konca zlatého obdĺžnika odreže štvorec, potom druhý koniec je nový zlatý obdĺžnik. Na obrázku je veľký obdĺžnik (modrý a ružový spolu) zlatý obdĺžnik, pretože a / b = φ {\displaystyle a/b=\varphi } 
. Modrá časť (B) je štvorec. Ružová časť sama o sebe (A) je ďalší zlatý obdĺžnik, pretože b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } 
. Veľký obdĺžnik a ružový obdĺžnik majú rovnaký tvar, ale ružový obdĺžnik je menší a je otočený.
Veľký obdĺžnik BA je zlatý obdĺžnik; to znamená, že pomer b:a je 1: φ {\displaystyle \varphi } . Pre každý takýto obdĺžnik, a to len pre obdĺžniky s týmto konkrétnym pomerom, platí, že ak odstránime štvorec B, zostane A, teda ďalší zlatý obdĺžnik, t. j. s rovnakým pomerom ako pôvodný obdĺžnik.
Fibonacciho čísla
Fibonacciho čísla sú zoznamom čísel. Ďalšie číslo v zozname nájde človek tak, že posledné dve čísla sčíta. Ak človek vydelí číslo v zozname číslom, ktoré mu predchádzalo, tento pomer sa stále viac približuje zlatému rezu.
| Fibonacciho číslo | delené predchádzajúcim | pomer |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\displaystyle \varphi } | = 1.6180... |
Zlatý rez v prírode
V prírode sa zlatý rez často používa pri usporiadaní listov alebo kvetov. Tie využívajú zlatý uhol približne 137,5 stupňa. Listy alebo kvety usporiadané v tomto uhle najlepšie využívajú slnečné svetlo.
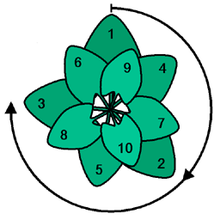
Použitie zlatého uhla optimálne využije slnečné svetlo. Toto je pohľad zhora.
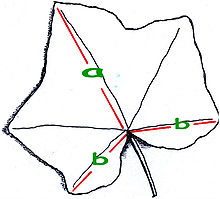
List brečtanu obyčajného, ktorý znázorňuje zlatý rez
Otázky a odpovede
Otázka: Aký je pomer dvoch čísel?
Odpoveď: Pomer dvoch čísel zistíme ich delením, takže pomer bude a/b.
Otázka: Ako sa dá nájsť iný pomer?
Odpoveď: Ďalší pomer sa dá nájsť tak, že dve čísla sčítame a tento súčet vydelíme väčším číslom a. Tento nový pomer by bol (a+b)/a.
Otázka: Ako sa nazýva prípad, keď sa tieto dva pomery navzájom rovnajú?
Odpoveď: Keď sa tieto dva pomery navzájom rovnajú, nazýva sa to zlatý rez. Zvyčajne sa znázorňuje gréckym písmenom צ alebo phi.
Otázka: Ak b = 1 a a/b = צ , čo to znamená pre a?
Odpoveď: Ak b = 1 a a/b = צ , potom to znamená, že aj a = צ.
Otázka: Ako sa dá toto číslo zapísať?
Odpoveď: Jeden zo spôsobov zápisu tohto čísla je צ = 1 + 5 / 2 = 1,618...
Otázka: Čo znamená, ak od neho odčítame 1 alebo ním vydelíme 1?
Odpoveď: Ak od neho odčítaš 1 alebo ním vydelíš 1, dostaneš späť to isté číslo - inými slovami, obe sa budú rovnať zlatému rezu.
Otázka: Je zlatý rez iracionálne číslo?
Odpoveď: Áno, zlatý podiel je iracionálne číslo, čo znamená, že ak sa ho niekto pokúsi zapísať, nikdy nebude mať koniec a žiadny vzor - bude sa začínať len niečím ako "1,6180339887...".
Prehľadať