Funkcia hustoty pravdepodobnosti

Funkcia hustoty pravdepodobnosti je funkcia, ktorú možno definovať pre akékoľvek spojité rozdelenie pravdepodobnosti. Integrál funkcie hustoty pravdepodobnosti v intervale [ a , b ] {\displaystyle [a,b]} $[a,b]$ dáva pravdepodobnosť, že daná náhodná premenná s danou hustotou sa nachádza v danom intervale.

Funkcia hustoty pravdepodobnosti je potrebná na prácu so spojitými rozdeleniami. Pri hode kockou dostaneme čísla 1 až 6 s pravdepodobnosťou 1 6 {\displaystyle {\tfrac {1}{6}}} ${\tfrac {1}{6}}$ , ale toto nie je spojitá funkcia, pretože možné sú len čísla 1 až 6. Naopak, dvaja ľudia nebudú mať rovnakú výšku alebo rovnakú hmotnosť. Pomocou funkcie hustoty pravdepodobnosti je možné určiť pravdepodobnosť pre ľudí s výškou medzi 180 cm a 181 cm alebo medzi 80 kg a 81 kg, hoci medzi týmito dvoma hranicami je nekonečne veľa hodnôt.

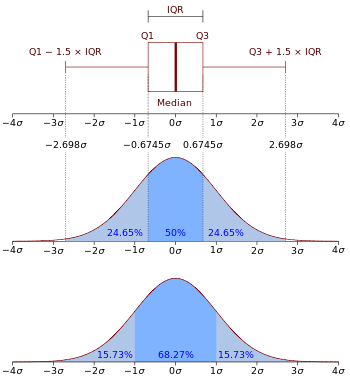
Boxplot a funkcia hustoty pravdepodobnosti normálneho rozdelenia N(0, σ2) .

Otázky a odpovede

Otázka: Čo je to funkcia hustoty pravdepodobnosti?

Odpoveď: Funkcia hustoty pravdepodobnosti je funkcia, ktorá charakterizuje akékoľvek spojité rozdelenie pravdepodobnosti.

Otázka: Ako sa zapisuje funkcia hustoty pravdepodobnosti náhodnej premennej X?

Odpoveď: Funkcia hustoty pravdepodobnosti X sa niekedy zapisuje ako f_X(x).

Otázka: Čo predstavuje integrál funkcie hustoty pravdepodobnosti?

Odpoveď: Integrál funkcie hustoty pravdepodobnosti predstavuje pravdepodobnosť, že daná náhodná premenná s danou hustotou sa nachádza v danom intervale.

Otázka: Je funkcia hustoty pravdepodobnosti vždy nezáporná v celej svojej oblasti?

Odpoveď: Áno, podľa definície je funkcia hustoty pravdepodobnosti nezáporná v celej svojej oblasti.

Otázka: Je súčet integrácie cez interval rovný 1?

Odpoveď: Áno, integrácia cez interval sa rovná 1.

Otázka: Aký typ rozdelenia charakterizuje funkcia hustoty pravdepodobnosti?

Odpoveď: Funkcia hustoty pravdepodobnosti charakterizuje akékoľvek spojité rozdelenie pravdepodobnosti.