Smerodajná odchýlka
Štandardná odchýlka je číslo, ktoré sa používa na určenie toho, ako sú merania skupiny rozptýlené od priemeru (strednej hodnoty) alebo očakávanej hodnoty. Nízka štandardná odchýlka znamená, že väčšina čísel je blízko priemeru. Vysoká štandardná odchýlka znamená, že čísla sú viac rozptýlené.
Uvádzaná chybovosť je zvyčajne dvojnásobok štandardnej odchýlky. Vedci bežne uvádzajú štandardnú odchýlku čísel od priemerného čísla pri experimentoch. Často sa rozhodnú, že dôležité sú len rozdiely väčšie ako dvoj- alebo trojnásobok štandardnej odchýlky. Štandardná odchýlka je užitočná aj v peňažníctve, kde štandardná odchýlka zarobených úrokov ukazuje, ako sa môžu líšiť zarobené úroky jednej osoby od priemeru.
Mnohokrát je možné merať len vzorku alebo časť skupiny. Potom sa dá číslo blízke smerodajnej odchýlke pre celú skupinu zistiť pomocou trochu odlišnej rovnice, ktorá sa nazýva smerodajná odchýlka vzorky, vysvetlená nižšie.
.png)
Graf normálneho rozdelenia (alebo zvonovej krivky). Každý farebný pás má šírku jednej štandardnej odchýlky.
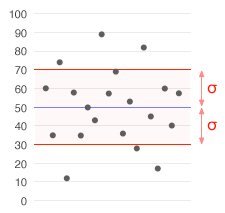
Súbor údajov s priemerom 50 (znázornený modrou farbou) a štandardnou odchýlkou (σ) 20.
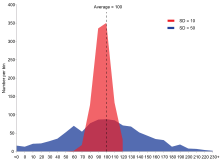
Príklad dvoch výberových populácií s rovnakým priemerom a rôznymi štandardnými odchýlkami. Červená populácia má priemer 100 a SD 10; modrá populácia má priemer 100 a SD 50.
Základný príklad
Uvažujme skupinu, ktorá má nasledujúcich osem čísel:
2 , 4,4 ,4 , 5, , 5, 7{\displaystyle9 2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9}
Týchto osem čísel má priemer (mean) 5:
2 + +4 +4 +4 +5 + + 57= 98{\displaystyle5 {\frac {2+4+4+4+5+5+7+9}{8}}=5}
Ak chcete vypočítať štandardnú odchýlku populácie, najprv zistite rozdiel každého čísla v zozname od priemeru. Výsledok každého rozdielu potom vyčíslite na druhú stranu:
(2 - 5) =2 ( - 3) =2 ( 95- 5) =2 = 02( 04-5 ) =2 ( - 1) =2 (15 - 5) =2 = 02( 04-5 ) = ( - ) = 2( - 1) = 2(17 - 5) =2 = 22( 44-5 ) = 2( -1 ) =2 ( 19- 5) = 2= 42{\displaystyle16 {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
Potom zistite priemer týchto hodnôt (súčet vydelený počtom čísel). Nakoniec urobte druhú odmocninu:
( +9 +1 +1 +1 + 0+ 0+ 4) 16= 8{\displaystyle2 {\sqrt {\frac {(9+1+1+1+1+0+0+4+16)}{8}}}=2}
Odpoveďou je štandardná odchýlka populácie. Vzorec je pravdivý len vtedy, ak osem čísel, s ktorými sme začali, je celá skupina. Ak sú len časťou náhodne vybranej skupiny, potom by sme mali v dolnej časti (menovateli) predposledného kroku použiť 7 (čo je n - 1) namiesto 8 (čo je n). Potom je odpoveďou výberová smerodajná odchýlka. Toto sa nazýva Besselova korekcia.
Ďalšie príklady
Trochu ťažší príklad z reálneho života: Priemerná výška dospelých mužov v Spojených štátoch je 70 cm so štandardnou odchýlkou 3 cm. Štandardná odchýlka 3" znamená, že väčšina mužov (približne 68 %, za predpokladu normálneho rozdelenia) má výšku o 3" vyššiu až 3" nižšiu ako je priemer (67"-73") - jedna štandardná odchýlka. Takmer všetci muži (približne 95 %) majú výšku o 6" vyššiu až 6" nižšiu ako priemer (64"-76") - dve štandardné odchýlky. Tri štandardné odchýlky zahŕňajú všetky čísla pre 99,7 % skúmanej vzorky populácie. To platí, ak je rozdelenie normálne (zvonové).
Ak by štandardná odchýlka bola nulová, potom by všetci muži boli vysokí presne 70". Ak by štandardná odchýlka bola 20", potom by niektorí muži boli oveľa vyšší alebo oveľa nižší ako priemer, s typickým rozpätím približne 50"-90".
Ďalší príklad: každá z troch skupín {0, 0, 14, 14}, {0, 6, 8, 14} a {6, 6, 8, 8} má priemer (strednú hodnotu) 7. Ich štandardné odchýlky sú však 7, 5 a 1. Tretia skupina má oveľa menšiu štandardnú odchýlku ako ostatné dve, pretože všetky jej čísla sú blízke 7. Základná myšlienka je, že štandardná odchýlka nám hovorí, ako ďaleko od priemeru majú zvyšné čísla tendenciu byť. Bude mať rovnaké jednotky ako samotné čísla. Ak napríklad skupina {0, 6, 8, 14} predstavuje vek skupiny štyroch bratov v rokoch, priemer je 7 rokov a štandardná odchýlka je 5 rokov.
Štandardná odchýlka môže slúžiť ako miera neistoty. Vo vede napríklad štandardná odchýlka skupiny opakovaných meraní pomáha vedcom zistiť, aká je istota priemerného čísla. Pri rozhodovaní o tom, či merania z experimentu súhlasia s predikciou, je štandardná odchýlka týchto meraní veľmi dôležitá. Ak je priemerné číslo z experimentov príliš vzdialené od predpovedaného čísla (pričom vzdialenosť sa meria v štandardných odchýlkach), potom testovaná teória nemusí byť správna. Pozri interval predpovede.
Príklady použitia
Štandardná odchýlka súboru hodnôt je užitočná na to, aby ste vedeli, aký veľký rozdiel od "priemeru" (strednej hodnoty) sa očakáva.
Počasie
Ako jednoduchý príklad uveďme priemerné denné vysoké teploty v dvoch mestách, jednom vo vnútrozemí a druhom v blízkosti oceánu. Je užitočné pochopiť, že rozsah denných vysokých teplôt v mestách v blízkosti oceánu je menší ako v mestách vo vnútrozemí. Každé z týchto dvoch miest môže mať rovnakú priemernú dennú teplotu. Štandardná odchýlka dennej vysokej teploty pre pobrežné mesto však bude menšia ako pre mesto vo vnútrozemí .
Šport
Ďalším spôsobom, ako sa na to pozrieť, je uvažovať o športových tímoch. V každom športe sa nájdu tímy, ktoré sú v niečom dobré a v niečom nie. Tímy, ktoré sa umiestnili najvyššie, nebudú vykazovať veľké rozdiely v schopnostiach. Darí sa im vo väčšine kategórií. Čím nižšia je štandardná odchýlka ich schopností v jednotlivých kategóriách, tým sú vyrovnanejšie a konzistentnejšie. Tímy s vyššou štandardnou odchýlkou však budú menej predvídateľné. Tím, ktorý je zvyčajne zlý vo väčšine kategórií, bude mať nízku štandardnú odchýlku. Tím, ktorý je zvyčajne dobrý vo väčšine kategórií, bude mať tiež nízku štandardnú odchýlku. Tím s vysokou štandardnou odchýlkou však môže byť typom tímu, ktorý získava veľa bodov (silný útok), ale zároveň umožňuje druhému tímu získať veľa bodov (slabá obrana).
Snaha zistiť dopredu, ktoré tímy vyhrajú, môže zahŕňať pohľad na štandardné odchýlky rôznych tímových "štatistík". Čísla, ktoré sa líšia od očakávaných, môžu zodpovedať silným a slabým stránkam, aby sa ukázalo, aké dôvody môžu byť najdôležitejšie pre poznanie, ktorý tím vyhrá.
Pri pretekoch sa meria čas, za ktorý jazdec dokončí každé kolo na trati. Jazdec s nízkou štandardnou odchýlkou času na kolo je konzistentnejší ako jazdec s vyššou štandardnou odchýlkou. Tieto informácie sa dajú použiť na pochopenie toho, ako môže vodič skrátiť čas potrebný na dokončenie kola.
Peniaze
V peňažníctve môže štandardná odchýlka znamenať riziko, že cena vzrastie alebo klesne (akcie, dlhopisy, nehnuteľnosti atď.). Môže tiež znamenať riziko, že skupina cien pôjde hore alebo dole (aktívne spravované podielové fondy, indexové podielové fondy alebo ETF). Riziko je jedným z dôvodov, prečo sa rozhodovať o tom, čo kúpiť. Riziko je číslo, pomocou ktorého môžu ľudia zistiť, koľko peňazí môžu zarobiť alebo stratiť. Čím je riziko väčšie, tým môže byť výnos z investície vyšší, ako sa očakáva (štandardná odchýlka "plus"). Investícia však môže aj stratiť viac peňazí, ako sa očakávalo (štandardná odchýlka "mínus").
Osoba si napríklad musela vybrať medzi dvoma akciami. Akcia A mala za posledných 20 rokov priemerný výnos 10 % so štandardnou odchýlkou 20 percentuálnych bodov (pp). Akcia B mala za posledných 20 rokov priemerný výnos 12 percent, ale vyššiu štandardnú odchýlku 30 p. b. Ak sa človek zamyslí nad rizikom, môže sa rozhodnúť, že akcia A je bezpečnejšia voľba. Aj keď možno nezarobí toľko peňazí, pravdepodobne ani veľa peňazí nestratí. Osoba si môže myslieť, že o 2 percentuálne body vyšší priemer akcie B nestojí za dodatočnú štandardnú odchýlku 10 p. b. (väčšie riziko alebo neistota očakávaného výnosu).
Pravidlá pre normálne rozdelené čísla
Väčšina matematických rovníc pre štandardnú odchýlku predpokladá, že čísla sú normálne rozdelené. To znamená, že čísla sú rozložené určitým spôsobom na oboch stranách priemernej hodnoty. Normálne rozdelenie sa nazýva aj Gaussovo rozdelenie, pretože ho objavil Carl Friedrich Gauss. Často sa nazýva zvonovitá krivka, pretože čísla sa rozložia tak, že na grafe vytvoria tvar zvona.
Čísla nie sú normálne rozdelené, ak sú zoskupené na jednej alebo druhej strane priemernej hodnoty. Čísla môžu byť rozložené a stále sú normálne rozdelené. Štandardná odchýlka hovorí, ako veľmi sú čísla rozložené.

Tmavomodrá farba je menej ako jedna štandardná odchýlka od priemeru. V prípade normálneho rozdelenia to zahŕňa 68,27 % čísel, zatiaľ čo dve štandardné odchýlky od priemeru (stredná a tmavomodrá) zahŕňajú 95,45 %, tri štandardné odchýlky (svetlá, stredná a tmavomodrá) zahŕňajú 99,73 % a štyri štandardné odchýlky predstavujú 99,994 %.
Vzťah medzi priemerom a štandardnou odchýlkou
Priemer (priemer) a štandardná odchýlka súboru údajov sa zvyčajne zapisujú spoločne. Potom človek pochopí, aké je priemerné číslo a ako veľmi sú ostatné čísla v skupine rozptýlené.
Rozloženie skupiny čísel možno vyjadriť aj variačným koeficientom, ktorý predstavuje štandardnú odchýlku vydelenú priemerom. Je to bezrozmerné číslo. Variačný koeficient sa často násobí 100 % a zapisuje sa ako percento.
História
Termín štandardná odchýlka prvýkrát písomne použil Karl Pearson v roku 1894 po tom, ako ho použil na prednáškach. Bolo to ako náhrada za predchádzajúce názvy pre tú istú myšlienku: napríklad Gauss používal strednú chybu.
Súvisiace stránky
- Presnosť a precíznosť
- Veľkosť vzorky
Otázky a odpovede
Otázka: Čo je to štandardná odchýlka?
Odpoveď: Štandardná odchýlka je číslo, ktoré sa používa na určenie toho, ako sú merania skupiny rozptýlené od priemeru (strednej alebo očakávanej hodnoty).
Otázka: Čo znamená nízka štandardná odchýlka?
Odpoveď: Nízka štandardná odchýlka znamená, že väčšina čísel je blízko priemeru.
Otázka: Čo znamená vysoká štandardná odchýlka?
Odpoveď: Vysoká štandardná odchýlka znamená, že čísla sú viac rozptýlené.
Otázka: Ako sa štandardná odchýlka používa v peniazoch?
Odpoveď: V peniazoch štandardná odchýlka dosiahnutých úrokov ukazuje, ako sa môžu líšiť dosiahnuté úroky jednej osoby od priemeru.
Otázka: Kedy možno merať len časť skupiny?
Odpoveď: Mnohokrát možno merať len vzorku alebo časť skupiny.
Otázka: Ako sa znázorňuje štandardná odchýlka celej skupiny?
Odpoveď: Štandardná odchýlka celej skupiny je reprezentovaná gréckym písmenom َ {\displaystyle \sigma } .
Otázka: Ako sa znázorňuje smerodajná odchýlka vzorky?
Odpoveď: Štandardná odchýlka vzorky je reprezentovaná písmenom s {\displaystyle s} .
Prehľadať



