Princíp neurčitosti

Diagramy

1. Fotóny, elektróny a iné subatomárne častice sa po vystrelení cez veľkú dieru zaostria, ale nevieme presne, kde sa nachádzali v polovici dráhy.


2. Zúženie otvoru ohýba dráhy častíc okolo okrajov otvoru (difrakcia), takže výsledný lúč je väčší a mäkší.


3. Zúženie otvoru zvyšuje istotu, kde sa fotón nachádza v strede, ale potom sa jeho smer odtiaľ k detekčnej obrazovke vpravo stáva primerane neistejším. Zaostrenie sa stáva neostrým. Rozšírenie diery spôsobí, že všetky fotóny skončia v strede detekčnej obrazovky, ale potom máme menšiu predstavu o tom, kde sa nachádzali, keď prešli stredovou bariérou.


4. Pružina upevnená na prekážke s malým otvorom spôsobí, že sa častica pretlačí cez otvor, čím sa pretlačí prekážka, natiahne pružiny, a tak sa zmeria hybnosť. Keďže sa však bariéra namontovaná na pružine pohybuje, máme menšiu istotu, kde sa častica nachádzala, keď prešla otvorom, a difrakcia tiež ovplyvní jej polohu na detekčnej obrazovke.


5. Zavesenie stredovej medzery pomocou pružinových váh umožňuje meranie hybnosti, ale medzera sa pritom nepredvídateľne posúva, takže sa stráca informácia o polohe každého fotónu v strede.


6. Táto animácia ukazuje jeden z dôležitých dôsledkov neurčitosti vesmíru: kvantové tunelovanie elektrónov. Pozorne sa pozrite. Zakaždým sa cez bariéru dostane malý kúsok.

Ako sa ľudia naučili o neistote?

Veľmi krátko po tom, čo Werner Heisenberg vytvoril novú kvantovú fyziku, sa priamo z jeho matematiky vynorilo niečo neočakávané, výraz:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad }

Rozsah chyby v polohe (x) krát rozsah chyby v hybnosti (p) je približne rovnaký alebo väčší ako Planckova konštanta delená 4π.

Tieto symboly vyjadrujú v matematickej podobe to, čo ste už videli na obrázkoch vyššie. Symboly jasne hovoria, že si nemôžete byť úplne istí, kde sa niečo nachádza a kam to smeruje. Ak máte jasnejšiu predstavu o tom, kde to v danom okamihu je, potom máte menšiu predstavu o tom, kam to ide a ako rýchlo. Ak si v ktoromkoľvek okamihu ujasníte, kam to ide a ako rýchlo, potom máte menšiu predstavu o tom, kde to je práve teraz.

Vedci už dávnejšie zistili, prečo niektoré látky vydávajú charakteristické farby svetla, keď sú zahriate alebo inak excitované. Heisenberg sa snažil vysvetliť, prečo má každá z týchto farieb charakteristický jas. Nebolo by dosť dobré, keby on a ostatní vedci len povedali: "No, tak to jednoducho je." Boli si istí, že pre tieto rozdiely musí existovať dobrý dôvod, ako aj pre to, že pomery medzi intenzitami jasových čiar sú pre každú vzorku prvku vždy rovnaké.

Netušil, že narazí na skryté tajomstvo prírody, keď sa pustí do objavovania vysvetlenia intenzity farebných čiar charakteristických pre jednotlivé prvky. Štúdium kvantovej mechaniky už ukázalo, prečo má vodík štyri jasné čiary v tej časti spektra, ktorú vidí človek. Muselo sa zdať, že ďalšou vecou, ktorú sa treba naučiť, je jednoducho vypočítať ich jas. Zdalo sa, že vodík je jasným začiatkom, pretože má len jeden elektrón, s ktorým sa treba vysporiadať, a len štyri čiary vo viditeľnej časti spektra. Určite musí existovať dobrý dôvod, prečo nie sú rovnako jasné. Vysvetlenie jasnosti rôznofarebných čiar neónu a ostatných prvkov mohlo počkať.

 

Heisenberg začal pracovať na kvantovej fyzike úpravou klasických rovníc pre elektrinu, ktoré sú na začiatku veľmi komplikované, takže matematika v jeho článku z roku 1925 bola veľmi náročná.

Snažil sa nájsť správny spôsob výpočtu intenzity jasných čiar v spektre vodíkovej lampy. Musel nájsť príbuznú veličinu nazývanú "amplitúda" a vynásobiť amplitúdu amplitúdou (alebo inými slovami musel amplitúdu odmocniť), aby získal požadovanú intenzitu. Musel prísť na to, ako vyjadriť amplitúdu spôsobom, ktorý zohľadňuje skutočnosť, že vodíkové lampy nevyžarujú na všetkých frekvenciách a nevyžarujú v súvislom rozsahu frekvencií v časti spektra, ktorú ľudia vidia. Heisenberg našiel nový pozoruhodný spôsob výpočtu amplitúdy.

Podivná rovnica|rovnica, ktorú Heisenberg objavil a použil na násobenie jednej kvantovej veličiny (napr. polohy) inou (napr. hybnosťou), bola uverejnená v takzvanom "Heisenbergovom 'magickom' článku z júla 1925".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

Vyššie uvedená matematika vyzerá veľmi ťažko, ale matematika, ktorá k nej vedie, je oveľa ťažšia a je veľmi ťažké ju pochopiť. Uvádzame ju tu len preto, aby sme ukázali, ako vyzerala. Heisenbergov článok je historickým medzníkom. Mnohí fyzici, ktorí si jeho článok prečítali, povedali, že nemôžu nesúhlasiť s jeho závermi, ale že nemôžu pochopiť jeho vysvetlenie, ako k týmto záverom dospel. Počiatočné rovnice, ktoré Heisenberg použil, zahŕňali Fourierove rady a obsahovali mnoho faktorov. K uvedenej rovnici sa ešte vrátime, pretože je to akýsi recept na zápis a násobenie matíc.

Nové rovnice museli byť také zvláštne a nezvyčajné, pretože Heisenberg opisoval zvláštny svet, v ktorom sa niektoré veci, napríklad dráhy elektrónov, pomaly nezväčšujú ani nezmenšujú. Nové druhy zmien zahŕňajú skoky a veľké medzery medzi skokmi. Elektróny môžu preskakovať len medzi určitými dráhami a energia získaná alebo stratená pri zmene medzi dráhami vzniká, keď sa pohltí fotón so správnou energiou alebo sa vytvorí nový fotón so správnou energiou. Ak elektróny v atómoch vodíka najčastejšie preskakujú (padajú) medzi dvoma konkrétnymi orbitmi, potom sa na tejto energetickej úrovni vyžiari viac fotónov, a preto bude svetlo produkované na tejto úrovni najintenzívnejšie.

Bolo ťažké prispôsobiť rovnice vytvorené pre spojité spektrá (to, čo vidíte, keď slnečné svetlo prechádzalo cez hranol) spektrám, ktoré majú len niekoľko špičkových frekvencií, medzi ktorými nie je nič. Takmer všetko, čo sa už o svetle a energii naučili, sa robilo s veľkými objektmi, ako sú horiace sviečky alebo slnko, a všetky tieto veľké objekty vytvárajú spojité spektrá. Aj keď sa s týmito vecami bežnej veľkosti dali ľahko robiť experimenty, trvalo ešte dlho, kým sa zistili zákony (fyziky), ktorými sa riadia. Teraz sa fyzici zaoberali vecami príliš malými na to, aby ich videli, vecami, ktoré nevytvárali spojité spektrá, a snažili sa nájsť spôsob, ako z toho, čo už vedeli, získať aspoň záchytné body, ktoré by im pomohli nájsť zákony týchto malých a medzerovitých zdrojov svetla.

Pôvodné rovnice sa týkali vibrujúceho telesa, ktoré by vytváralo vlny, podobne ako trstina v organe, ktorá by vytvárala zvukovú vlnu s charakteristickou frekvenciou. Takže tu bol pohyb dozadu a dopredu (ako pri vibrovaní trstiny) a vyžarovaná vlna, ktorú bolo možné zobraziť ako sínusoidu. Mnohé z toho, čo sa predtým zistilo o fyzike na úrovni atómov, súviselo s pohybom elektrónov okolo jadier. Keď sa hmota pohybuje po obežnej dráhe, keď sa otáča okolo nejakého náboja, má to, čo sa nazýva "uhlový moment". Uhlový moment je spôsob, akým sa niečo ako kolotoč bude ďalej otáčať aj po tom, ako ho ľudia prestanú tlačiť. Matematika používaná na výpočet fázy a uhlového momentu hybnosti je zložitá. Navyše Heisenberg vo svojom článku z roku 1925 neuviedol všetky svoje výpočty, takže aj dobrí matematici môžu mať problém doplniť to, čo neuviedol.

Hoci mnohí fyzici tvrdili, že nedokážu pochopiť jednotlivé matematické kroky v Heisenbergovom prelomovom článku, jeden nedávny článok, ktorý sa snaží vysvetliť, ako Heisenberg dospel k svojmu výsledku, má dvadsať strán plných matematiky. Ani tento článok nie je jednoduchý na pochopenie. Matematika sa začala naozaj ťažkými vecami a nakoniec by vyústila do niečoho relatívne jednoduchého, čo je uvedené v hornej časti tohto článku. Dostať sa k jednoduchšiemu výsledku nebolo jednoduché a my sa nebudeme snažiť ukázať proces, ako sa dostať od zastaraného obrazu vesmíru k novej kvantovej fyzike. Potrebujeme len toľko detailov, aby sme ukázali, že takmer hneď ako Heisenberg urobil svoj prelomový objav, objavila sa časť fungovania vesmíru, ktorú nikto predtým nevidel.

Heisenberg musel byť veľmi nadšený, ale aj veľmi unavený, keď neskoro v noci konečne urobil svoj prielom a začal si dokazovať, že to bude fungovať. Takmer hneď si všimol niečo zvláštne, niečo, čo považoval za nepríjemný malý problém, ktorý by mohol nejako odstrániť. Ukázalo sa však, že táto malá nepríjemnosť bola veľkým objavom.

Heisenberg pracoval na násobení amplitúd amplitúdami a teraz mal Heisenberg dobrý spôsob, ako vyjadriť amplitúdu pomocou svojej novej rovnice. Prirodzene, že premýšľal o násobení a o tom, ako by vynásobil veci, ktoré boli dané zložitými rovnicami.

Heisenberg si uvedomil, že okrem kvadratizácie amplitúdy bude nakoniec chcieť násobiť polohu hybnosťou alebo energiu časom, a zdalo sa, že bude mať význam, ak v týchto nových prípadoch otočí poradie. Heisenberg si nemyslel, že by malo záležať na tom, či človek násobí polohu hybnosťou alebo či násobí hybnosť polohou. Keby to boli len jednoduché čísla, nebol by v tom žiadny problém. Ale v oboch prípadoch išlo o komplikované rovnice a ukázalo sa, že spôsob, akým ste dostali čísla na dosadenie do rovníc, sa líšil podľa toho, ktorým spôsobom ste začali. V prírode ste museli zmerať polohu a potom zmerať hybnosť, alebo ste museli zmerať hybnosť a potom zmerať polohu, a v matematike prevládala rovnaká všeobecná situácia. (Ak sa chcete dozvedieť fušerské detaily, pozrite si článok Heisenberg's entryway to matrix mechanics na anglickej Wikipédii!) Drobné, ale otravné rozdiely medzi výsledkami mali zostať, bez ohľadu na to, ako veľmi si Heisenberg želal, aby zmizli.

Heisenberg sa vtedy nedokázal zbaviť tohto malého problému, ale bol vyčerpaný, a tak odovzdal svoju prácu svojmu priamemu nadriadenému Maxovi Bornovi a odišiel na dovolenku.

Max Born bol pozoruhodný matematik, ktorý si čoskoro všimol, že rovnica, ktorú mu dal Heisenberg, je akýmsi receptom na zápis matice. Doktor Born bol v tom čase jedným z mála ľudí, ktorí sa zaujímali o tento zvláštny druh matematiky, o ktorom si väčšina ľudí myslela, že sa na nič moc nehodí. Vedel, že matice sa dajú násobiť, takže vykonávanie všetkých výpočtov na započítanie jedného fyzikálneho problému sa dalo zvládnuť vynásobením jednej matice druhou. Práve schopnosť dať komplikovaný postup do štandardnej a prijateľnej podoby by mu uľahčila prácu. Mohlo by to tiež uľahčiť jeho akceptovanie inými ľuďmi.

Born bol taký dobrý matematik, že si takmer okamžite uvedomil, že zmena poradia násobenia oboch matíc by viedla k odlišnému výsledku a výsledky by sa líšili len o málo. Táto hodnota by bola h/2πi. V bežnom živote by bol tento rozdiel taký malý, že by sme ho ani nevideli.

Keď sú niektoré molekuly excitované, vydávajú charakteristickú farbu.


Vodíkové spektrum


Neónové spektrum


Celé vizuálne spektrum slnka. Neexistujú žiadne medzery. Tento graf zobrazuje intenzity pri rôznych frekvenciách.


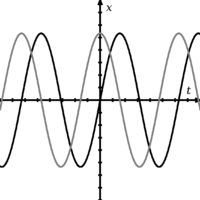
Dve vlny, ktoré sú navzájom mimo fázy

K formálnej teórii neurčitosti

Trvalo to niekoľko rokov, ale Heisenbergovi sa podarilo dokázať princíp neurčitosti, ktorý hovorí, že Δx × Δp = h/2, čo je číslo, ktoré vychádza z pôvodných rovníc, ale vynecháva π a i, ktoré súvisia so zmenami fázy. Heisenberg vysvetlil, že svoj princíp neurčitosti odvodil z tohto predchádzajúceho výsledku, keď v roku 1927 napísal článok, v ktorom túto teóriu predstavil.

Konštanta zapísaná ako h, nazývaná Planckova konštanta, je záhadné číslo, ktoré sa často vyskytuje, preto musíme pochopiť, čo je toto malé číslo. Číselne sa zvyčajne udáva ako 6,62607×10^-34 J s (joule sekundy). Je to teda veličina, ktorá zahŕňa energiu a čas.

Bol objavený, keď si Planck uvedomil, že energia dokonalého žiariča (nazývaného žiarič čierneho telesa) sa vyžaruje v jednotkách určitej veľkosti nazývaných "kvantá" (jednotné číslo tohto slova je "kvantum"). Vyžiarená energia sa vyžaruje ako fotóny a frekvencia fotónu je úmerná "úderu", ktorý vydáva. Rôzne frekvencie viditeľného svetla vnímame ako rôzne farby. Na fialovom konci spektra má každý fotón relatívne veľké množstvo energie; na červenom konci spektra má každý fotón relatívne malé množstvo energie. Spôsob výpočtu množstva energie fotónu je daný rovnicou E = hν (energia sa rovná Planckovej konštante krát "nu" alebo frekvencia).

Heisenbergov princíp neurčitosti Δx × Δp ≥ h nám hovorí, že vždy, keď sa snažíme určiť určité dvojice čísel, môžeme sa k nim len priblížiť, a že ak sa pokúsime objasniť jedno z nich, t. j. ak sa pokúsime zmenšiť Δx, aby sme mali lepšiu predstavu o polohe niečoho, potom budeme musieť dostať späť väčšie číslo pre druhé číslo z dvojice, a že veľkosť odchýlky týchto dvoch čísel úzko súvisí s h.

Ďalšia dvojica fyzikálnych veličín sa riadi vzťahom neurčitosti: ΔE × Δt ≥ h, a táto dvojica okrem iného naznačuje, že ak sa pozrieme do medzihviezdneho priestoru, na nejaké miesto, kde by sme vôbec nič neočakávali, a Δt budeme znižovať čoraz bližšie k nule, potom sa pre zachovanie rovnováhy uvedenej v rovnici ΔE musí čoraz viac zväčšovať - a zrazu sa môže objaviť niečo s hybnosťou práve na tento krátky časový úsek.

Ako sa dá vysvetliť táto neurčitosť (nedostatok istoty)? Čo sa deje vo vesmíre? Často sa hovorí, že nová teória, ktorá je úspešná, môže poskytnúť nové informácie o skúmaných javoch. Heisenberg vytvoril matematický model, ktorý predpovedal správne intenzity pre spektrum jasnej čiary vodíka, ale bez toho, aby to zamýšľal, zistil, že určité dvojice fyzikálnych veličín odhaľujú neočakávanú neurčitosť. Až dovtedy nikto netušil, že merania nemožno donekonečna spresňovať a spresňovať. Skutočnosť, že ich nemožno urobiť istejšími, presnejšími, bola ohromujúcim novým objavom. Mnohí ľudia ho neboli ochotní prijať.

Bohr a jeho kolegovia tvrdili, že fotóny, elektróny atď. nemajú ani polohu, ani hybnosť, kým nie sú zmerané. Toto teoretické stanovisko vyplynulo z objavu neurčitosti a nebolo len nejakou osobnou preferenciou, čomu veriť. Bohr povedal, že o niečom, ako je fotón alebo elektrón, nevieme nič, kým to nepozorujeme. Na to, aby sme takúto malú vec mohli pozorovať, musíme s ňou nejako interagovať. V každodennom živote je možné robiť niečo také, ako chodiť vedľa automobilu a pritom si značiť časy, keď prechádza cez body na mriežke nakreslenej na chodníku. Možno samotná hmotnosť automobilu bude stláčať malé páčky v chodníku, ktoré vypnú hodiny pripevnené na každej z nich a zaznamenajú hmotnosť automobilu. Nakoniec by sme mali jasný záznam o tom, kde sa auto v rôznych časoch nachádzalo, a tiež by sme mohli vypočítať smer jeho postupu a hmotnosť. V každom okamihu na hodinách by sme tak mohli zistiť jeho polohu aj hybnosť (rýchlosť vynásobenú hmotnosťou). Ani by nás nenapadlo, že sila potrebná na pohyb malých páčok bude mať nejaký vplyv na postup auta. Takisto by sme si nepredstavovali, že automobil nemá žiadnu polohu ani trajektóriu medzi bodmi na chodníku, kde sú páčky, alebo že automobil v tých časoch existuje v akejsi trojrozmernej škvrne a ustáli sa len počas stláčania páčky. Svet, ktorý poznáme, neodhaľuje tieto zvláštne druhy interakcií.

Na lokalizáciu lode na mori počas najtmavšej noci by sme mohli použiť reflektor a toto svetlo by nenarušilo polohu ani smer pohybu lode, ale lokalizácia elektrónu pomocou svetla by si vyžadovala zasiahnuť ho jedným alebo viacerými fotónmi, z ktorých každý by mal dostatočnú hybnosť, aby narušil polohu a trajektóriu elektrónu. Lokalizácia elektrónu inými prostriedkami by si vyžadovala držať ho v nejakom fyzickom obmedzení, ktoré by tiež ukončilo jeho pohyb vpred.

Ak chcete lokalizovať fotón, najlepšie, čo môžete urobiť bez toho, aby ste ukončili jeho pohyb vpred, je prinútiť ho prejsť kruhovým otvorom v bariére. Ak poznáme čas, v ktorom bol fotón vyslaný (napríklad laserom), a čas, v ktorom fotón dorazí na detekčnú obrazovku, ako je digitálna kamera, potom je možné vypočítať čas potrebný na prekonanie tejto vzdialenosti a čas, v ktorom fotón prechádzal otvorom. Aby ním však fotón mohol prejsť, musí mať kruhový otvor priemer väčší, ako je veľkosť fotónu. Čím menšia je kruhová diera, tým bližšie sa priblížime k poznaniu presnej polohy fotónu pri jeho prechode. Nikdy však nemôžeme vedieť, či je fotón v tom čase mimo stredu. Ak je diera presne rovnako veľká ako fotón, neprechádza ňou. Keď sa priemer diery zmenšuje, hybnosť alebo smer fotónu pri jeho odchode z diery sa čoraz výraznejšie mení.

Niels Bohr a jeho kolegovia tvrdili, že sa dostávame do veľkých problémov, ak o veciach, ktoré sú príliš malé na to, aby sme ich mohli vidieť aj mikroskopom, predpokladáme, že sú pravdivé, čokoľvek, o čom máme dôkaz len v meradle každodenného života. V každodennom živote majú veci vždy určitú polohu. V atómovom meradle nemáme na podporu tohto záveru žiadny dôkaz. V každodennom živote majú veci určitý čas, v ktorom sa vyskytujú. V atómovom meradle nemáme na podporu tohto záveru žiadne dôkazy. Ak v každodennom živote pozorujeme továreň od nočnej zmeny prvého dňa po dennú zmenu druhého dňa a vidíme hotový automobil, ktorý sa vyvalil na expedičný dok, nemalo by zmysel tvrdiť, že nie je možné povedať, či bol dodaný počas nočnej alebo dennej zmeny. Ale na atómovej škále môžeme ukázať prípady, keď musíme počítať jeden fotón ako vyrobený v dvoch časoch. (Ak to nie je dosť zlé, môžeme ukázať aj prípady, keď je jeden fotón vyprodukovaný dvoma susednými lasermi.)

Časť ťažkostí pri zisťovaní, čo sa deje na atómovej úrovni, spočíva v tom, že by sme chceli vedieť, kde sa niečo nachádza a aká je jeho trajektória, a vedieť obe veci v rovnakom čase, ale nemôžeme merať polohu aj trajektóriu súčasne. Buď zmeriame hybnosť fotónu alebo elektrónu v jednom okamihu a potom bez väčšieho oneskorenia, ako je potrebné, zmeriame jeho polohu, alebo si to vymeníme a najprv zmeriame polohu a potom hybnosť. Problém je v tom, že tým, že prvé meranie nadobudne celkom určitý tvar (nejakým spôsobom ho stlačíme), zvýšime neistotu spojenú s ďalším meraním. Ak by naše počiatočné merania boli také hrubé, že by sa do každého z nich vnieslo veľa chýb, potom by sme mohli veci zlepšiť tým, že by sme pri každom z nich použili ľahší dotyk, ale nikdy by sme sa nedostali za určitú hranicu presnosti.

Z každodenného života vieme, že pokus o váženie na kúpeľňovej váhe umiestnenej na práčke v cykle odstreďovania prinesie nepresné výsledky, pretože ručička na váhe sa bude silno chvieť. Môžeme práčku vypnúť. Ak však chceme vykonať veľmi presné merania, zistíme, že ihla sa chveje aj pri prejazde nákladných áut v okolí, preto môžeme váhu položiť na niečo, čo ju izoluje od vonkajších rušivých vplyvov. Veríme, že sa nám podarí eliminovať vibrácie natoľko, aby sme dosiahli presne také výsledky, aké chceme. Nikdy neuvažujeme o tom, že vec na váhe sama vibruje alebo že má neurčitú hybnosť.

Ak vychádzame z princípu neurčitosti, zdá sa, že v skutočnosti neexistuje žiadna definitívna poloha a žiadna definitívna hybnosť pre akúkoľvek vec v atómovom meradle a že experimentátori môžu prinútiť veci k definitívnosti len v rámci limitu stanoveného princípom neurčitosti. Bohr a jeho kolegovia iba tvrdili, že bez meraní nemôžeme nič vedieť, a keď sa merania vykonajú, môžeme veci posunúť smerom k definitívnejšej polohe alebo definitívnejšej hybnosti, ale nemôžeme získať absolútnu definitívnosť alebo istotu, ktorú by sme chceli. Iní však túto možnosť brali vážne a tvrdili, že ak je matematika správna, potom vo svete ultra malého nemôže existovať definitívnosť alebo istota. Podstata vedy spočíva v tom, že matematika je len modelom reality a neexistuje žiadna záruka, že je to správny model.

Matematika a praktické dôsledky vecí, ktoré matematika predpovedá, sú také spoľahlivé, že je veľmi ťažké s nimi nesúhlasiť, ale to, čo matematika hovorí o skutočnom svete, prinieslo niekoľko rôznych názorov. Medzi vedcami, ktorí pracovali s Nielsom Bohrom v Kodani, sa princíp neurčitosti chápal tak, že na elementárnej úrovni fyzikálny vesmír neexistuje v deterministickej podobe. Je skôr súborom pravdepodobností alebo potenciálov.

V protiklade k príbehu, ktorý okolo matematiky utkala kodanská skupina, existujú aj iné príbehy, napríklad "interpretácia viacerých vesmírov", ktorá hovorí, že vždy, keď podľa kvantovej teórie existuje viacero možných výsledkov, každý výsledok sa vyskytuje vo vlastnom novom vesmíre. Einstein tvrdil, že viacero možných výsledkov neexistuje, takže existuje len jeden vesmír a ten je determinovaný, alebo, ako povedal, "Boh nehrá v kocky".

Ak by h bolo najmenším možným množstvom energie, potom by základná rovnica zobrazujúca energiu obsiahnutú vo fotónoch s rôznou frekvenciou nebola v rovnováhe. Bola by nesprávna.

Námietky proti princípu neurčitosti

Albert Einstein si všimol, že nová kvantová mechanika predpokladá nedostatok polohy a hybnosti v čase pred uskutočnením meraní, a dôrazne proti tomu namietal. Pevne veril, že veci mali pred meraním definitívne polohy a definitívne hybnosti a že skutočnosť, že meranie jednej z dvojice vecí a narušenie možnosti presného merania druhej veci netvrdí, že pred meraním chýbala jedna z nich. Spolu so svojimi dvoma kolegami napísal dokument, ktorý sa stal známy ako "EPR článok". Tento článok tvrdí, že musia existovať vlastnosti, ktoré určujú polohu a hybnosť, a že ak by sme ich mohli vidieť alebo ak by sme o nich mohli získať informácie, potom by sme mohli matematicky poznať a predpovedať polohu a hybnosť. Ľudia si dlho mysleli, že neexistuje spôsob, ako dokázať alebo vyvrátiť to, čo bolo pre Einsteina článkom viery. Tento spor bol veľmi produktívny, pretože viedol k všetkým moderným vývojom v oblasti entanglementu.

Z matematického hľadiska sa Einstein mýlil. V roku 1964 John Stewart Bell vyvinul matematickú metódu na rozlíšenie správania dvoch častíc, ktoré majú determinované stavy, ktoré sú neznáme len pre dve osoby, ktoré ich skúmajú, a dvoch častíc, ktoré majú prepletené stavy, ktoré sú neurčité alebo neisté, kým sa nezmerajú. Jeho metóda ukazuje, že pravdepodobnosti získania určitých výsledkov sú za týchto dvoch rôznych predpokladov rozdielne. Jeho práca sa nazýva Bellova veta alebo Bellova nerovnosť. Experimenty ukázali, že príroda sa správa tak, ako ju Bell opisuje.

Ďalšia cesta k neistote

Pôvodné diskusie o Heisenbergovom princípe neurčitosti vychádzali z modelu, ktorý neuvažoval o tom, že častice hmoty, ako sú elektróny, protóny atď., majú vlnovú dĺžku. V roku 1926 Louis de Broglie ukázal, že všetky veci, nielen fotóny, majú svoju vlastnú frekvenciu. Veci majú vlnovú a časticovú povahu, rovnako ako fotóny. Ak by sme sa pokúsili vlnu veci, ako je protón, zúžiť a zvýšiť, zjasnila by sa jej poloha, ale potom by sa hybnosť stala menej definovanou. Ak sa pokúsime spresniť časť opisu hybnosti vlny, t. j. dosiahnuť, aby zostala v užšom rozsahu hodnôt, potom sa vrchol vlny rozšíri a jej poloha sa stane menej určitou.

Vlna, ktorá je súčasťou opisu fotónu, nie je v kvantovej mechanike rovnaká ako vlna na hladine oceánu alebo oblasti stlačeného a zriedeného vzduchu, ktoré tvoria zvukové vlny. Namiesto toho majú tieto vlny vrcholy alebo oblasti s vysokou amplitúdou, ktoré súvisia s pravdepodobnosťou, že sa v danom bode v priestore a čase niečo nachádza. Presnejšie povedané, je to štvorec amplitúdy, ktorý udáva pravdepodobnosť objavenia sa nejakého javu.

Vlna, ktorá sa vzťahuje na fotón, môže byť čistá sínusoida. V takom prípade by štvorica hodnoty každého vrcholu udávala pravdepodobnosť pozorovania fotónu v danom bode. Keďže amplitúdy sínusových vĺn sú všade rovnaké, pravdepodobnosť nájdenia fotónu v každom z nich by bola rovnaká. Prakticky povedané, znalosť vlny pre jeden z týchto fotónov by teda neposkytla žiadnu informáciu o tom, kde ho treba hľadať. Na druhej strane hybnosť fotónu matematicky súvisí s amplitúdou jeho vlny. Keďže v tomto prípade máme čistú sínusoidu, amplitúda každého cyklu vlny je rovnaká, a preto je s touto vlnou spojená len jedna hodnota hybnosti. Nevedeli by sme, kam fotón dopadne, ale vedeli by sme presne, ako silno dopadne.

V lúčoch svetla, ktoré sa sústreďujú na určitý bod na detekčnej obrazovke, nie sú vlny spojené s fotónmi čistými sínusovými vlnami. Namiesto toho sú to vlny s vysokou amplitúdou v jednom bode a oveľa nižšími amplitúdami po oboch stranách tohto najvyššieho vrcholu. Matematicky je možné takúto vlnu analyzovať na množstvo rôznych sínusových vĺn s rôznymi vlnovými dĺžkami. O niečo jednoduchšie je predstaviť si opačný proces, keď sa pozrieme na počiatočnú sínusoidu jednej frekvencie, ku ktorej sa pridá druhá sínusoida inej vlnovej dĺžky, potom tretia, potom štvrtá atď. Výsledkom bude komplexná vlna vykazujúca jeden vysoký vrchol a obsahujúca veľký počet vĺn s rôznymi vlnovými dĺžkami, a teda s rôznymi momentmi. V takom prípade je pravdepodobnosť, že sa fotón objaví v určitom bode, mimoriadne vysoká, ale môže sa ukázať, že hybnosť, ktorú dodá, súvisí s vlnovou dĺžkou ktorejkoľvek zo zložiek vlny. Inými slovami, hodnota p = ħ/λ už nie je jedinou hodnotou, pretože treba brať do úvahy všetky dĺžky zostavených "vĺn s rôznou vlnovou dĺžkou".

Simulácia ukazuje, ako matematicky modelovať zostrenie polohy častice: Na pôvodnú sínusovú vlnu naneste mnoho rôznych vlnových foriem. Stred bude tvoriť čoraz vyšší vrchol a počet ostatných vrcholov sa bude zvyšovať, ale ich výška sa bude znižovať, pretože budú navzájom interferovať. Takže nakoniec je v superpozícii veľa rôznych vĺn, každá s inou vlnovou dĺžkou a (podľa p = ħ/λ) s inou hybnosťou, ale len jeden veľmi vysoký vrchol, ktorý rastie a zužuje sa a dáva nám niečo, čo je čoraz bližšie k určitej polohe.

Ak by sme chceli dosiahnuť čoraz väčšiu určitosť hybnosti, museli by sme odoberať čoraz viac a viac na seba navrstvených sínusoid, až by nám zostala len jednoduchá sínusoida. Pritom by sme postupne zmenšovali výšku centrálneho vrcholu a postupne zväčšovali výšky konkurenčných miest, kde by sme mohli nájsť časticu.

Keď teda začneme s vlnovým obrazom subatomárnych častíc, zvyčajne sa vždy budeme zaoberať prípadmi s relatívne vysokými centrálnymi vrcholmi a relatívne veľkým počtom vlnových dĺžok zložiek. Za týchto okolností nikdy nebude možné predpovedať presnú polohu alebo presnú hybnosť. Ak je matematický model presnou reprezentáciou skutočného sveta, potom žiadny fotón ani iná subatomárna častica nemá ani presnú polohu, ani určitú hybnosť. Keď takúto časticu meriame, môžeme si vybrať metódu, ktorá ešte viac stlačí pík a zúži ho, alebo si môžeme vybrať metódu, ktorá pík zníži a vyrovná vlnové dĺžky zložiek. V závislosti od toho, čo meriame a ako to meriame, môžeme dosiahnuť, aby naša poloha vyšla definitívnejšia, alebo aby sme zúžili rozsah hybnosti. Pri navrhovaní experimentu môžeme dbať na to, aby sme sa vyhli rôznym spôsobom rozhádzania aparatúry, ale nemôžeme sa zbaviť toho, že na začiatku nebolo nič úplne definitívne.

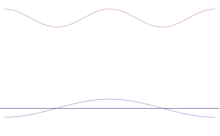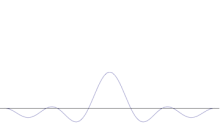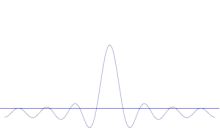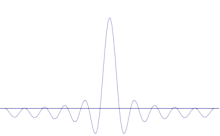
Superpozícia niekoľkých rovinných vĺn. Vlnový balík sa s pridaním mnohých vĺn stáva čoraz viac lokalizovaným. Fourierova transformácia je matematická operácia, ktorá rozdeľuje vlnový balík na jednotlivé rovinné vlny. Všimnite si, že vlny tu zobrazené sú reálne len na ilustračné účely, zatiaľ čo v kvantovej mechanike je vlnová funkcia vo všeobecnosti komplexná.

Kultúrne vplyvy

Najdôležitejší vplyv Heisenbergovho princípu neurčitosti bol na argumenty o slobode vôle. V rámci teórií klasickej fyziky je možné tvrdiť, že zákony príčiny a následku sú neúprosné a že ak raz vesmír začal určitým spôsobom, interakcie všetkej hmoty a energie, ktoré sa vyskytnú v budúcnosti, sa dajú vypočítať z tohto počiatočného stavu. Keďže všetko je absolútne dôsledkom toho, čo tomu predchádzalo, tvrdili, že každé rozhodnutie, ktoré človek urobí, a každá situácia, do ktorej sa človek dostane, bola predurčená od počiatku času. Nemáme teda žiadnu možnosť voľby v tom, čo robíme.

Ľudia, ktorí veria v slobodu vôle, tvrdia, že zákony kvantovej mechaniky nepredpovedajú, čo sa stane, ale len to, čo je viac a čo menej pravdepodobné. Preto je každý čin výsledkom série náhodných "hodov mincou" a žiadne rozhodnutie nemožno vysledovať na základe súboru nevyhnutných predpokladov.

Výrazy "kvantový skok" a "kvantový skok" sa stali bežnými spôsobmi hovorenia o veciach. Zvyčajne majú ľudia v úmysle opísať niečo, čo zahŕňa obrovskú zmenu, ku ktorej dôjde v krátkom čase. Tento výraz sa v skutočnosti vzťahuje na spôsob, akým sa chová elektrón v atóme, keď absorbuje fotón prichádzajúci zvonku, a tak preskočí z jednej obežnej dráhy okolo jadra atómu na vyššiu obežnú dráhu, alebo keď vyžiari fotón, a tak spadne z vyššej obežnej dráhy na nižšiu. Myšlienka Neilsa Bohra a jeho kolegov bola, že elektrón sa nepohybuje medzi obežnými dráhami, ale namiesto toho zmizne z jednej obežnej dráhy a okamžite sa objaví na inej obežnej dráhe. Kvantový skok teda v skutočnosti nie je nejaká zdrvujúca zmena, ale náhla malá zmena z jednej oblasti do druhej.

Keď ľudia merajú nejaký proces na subatomárnej úrovni a prejaví sa princíp neurčitosti, potom možno povedať, že ľudská činnosť ovplyvnila meranú vec. Vykonanie merania, ktorého cieľom je získať jednoznačný údaj o polohe častice, nevyhnutne ovplyvní jej hybnosť a nech sa urobí čokoľvek, aby sa táto hybnosť zmerala čo najskôr po zmeraní jej polohy, nemôže sa nezmeniť pravdepodobnosť toho, aká hybnosť sa zistí. Princíp neurčitosti teda dokáže vysvetliť niektoré druhy interferencií vyvolaných bádateľmi, ktoré ovplyvňujú výsledky experimentu alebo pozorovania. Nie všetky efekty pozorovateľa sú však spôsobené kvantovými efektmi alebo princípom neurčitosti. Zvyšné sú "efekty pozorovateľa", ale nie kvantové efekty neurčitosti.

Pozorovacie efekty zahŕňajú všetky druhy vecí, ktoré pôsobia v našom bežnom ľudskom meradle udalostí. Ak sa antropológ snaží získať jasnú predstavu o živote v primitívnej spoločnosti, ale jeho prítomnosť rozruší komunitu, ktorú navštívil, potom môžu byť jeho pozorovania veľmi zavádzajúce. Žiadna z relevantných interakcií však neprebieha na úrovni, ktorú opisuje kvantová mechanika alebo princíp neurčitosti.

Niekedy sa slovo "kvantový" používa na reklamné účely na označenie niečoho nového a výkonného. Napríklad výrobca malých benzínových motorov Briggs and Stratton má jeden rad štvorvalcových motorov s nízkym výkonom pre benzínové kosačky a podobné záhradné náradie, ktorý nazýva "Quantum".

Viac informácií

• Úvod do kvantovej teórie, s. 115 a s. 158

J.P. McEvoy a Oscar Zarate