Planckova konštanta

Pozadie

Symboly použité v tomto článku.
Symbol Význam E Energia h Planckova konštanta k Boltzmannova konštanta c rýchlosť svetla λ vlnová dĺžka žiarenia ν frekvencia žiarenia T absolútna teplota

V rokoch 1670 až 1900 vedci diskutovali o podstate svetla. Niektorí vedci sa domnievali, že svetlo sa skladá z mnohých miliónov malých častíc. Iní vedci sa domnievali, že svetlo je vlna.

Svetlo: vlny alebo častice?

V roku 1678 napísal Christiaan Huygens knihu Traité de la lumiere ("Pojednanie o svetle"). Veril, že svetlo sa skladá z vĺn. Tvrdil, že svetlo sa nemôže skladať z častíc, pretože svetlo z dvoch lúčov sa od seba neodráža. V roku 1672 napísal Isaac Newton knihu Opticks. Veril, že svetlo sa skladá z červených, žltých a modrých častíc, ktoré nazval telieska. Newton to vysvetlil svojím "experimentom s dvoma hranolmi". Prvý hranol rozdelil svetlo na rôzne farby. Druhý hranol tieto farby opäť spojil do bieleho svetla.

V 18. storočí sa najväčšia pozornosť venovala Newtonovej teórii. V roku 1803 Thomas Young opísal "dvojštrbinový experiment". Pri tomto experimente svetlo prechádzajúce cez dve úzke štrbiny interferuje samo so sebou. Vzniká tak obrazec, ktorý dokazuje, že svetlo sa skladá z vĺn. Po zvyšok devätnásteho storočia sa vlnovej teórii svetla venovala najväčšia pozornosť. V 60. rokoch 19. storočia James Clerk Maxwell vypracoval rovnice, ktoré opisovali elektromagnetické žiarenie ako vlny.

Teória elektromagnetického žiarenia považuje svetlo, rádiové vlny, mikrovlny a mnoho ďalších typov vĺn za to isté, len majú rôzne vlnové dĺžky. Vlnová dĺžka svetla, ktoré vidíme našimi očami, je približne 400 až 600 nm. Vlnová dĺžka rádiových vĺn sa pohybuje od 10 m do 1500 m a vlnová dĺžka mikrovĺn je približne 2 cm. Vo vákuu sa všetky elektromagnetické vlny šíria rýchlosťou svetla. Frekvencia elektromagnetického vlnenia je daná vzťahom:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}} .

Symboly sú definované tu.

Čierne telesá radiátorov

Všetky teplé veci vyžarujú tepelné žiarenie, ktoré je elektromagnetickým žiarením. Pre väčšinu vecí na Zemi je toto žiarenie v infračervenom pásme, ale niečo veľmi horúce (1000 °C alebo viac) vydáva viditeľné žiarenie, teda svetlo. Koncom 19. storočia mnohí vedci skúmali vlnové dĺžky elektromagnetického žiarenia zo žiaričov čierneho telesa pri rôznych teplotách.

Právo Rayleigh-Jeans

Lord Rayleigh prvýkrát uverejnil základy Rayleighovho-Jeansovho zákona v roku 1900. Teória bola založená na kinetickej teórii plynov. Sir James Jeans uverejnil úplnejšiu teóriu v roku 1905. Zákon súvisí s množstvom a vlnovou dĺžkou elektromagnetickej energie, ktorú vyžaruje žiarič čierneho telesa pri rôznych teplotách. Rovnica, ktorá ho opisuje, znie:

B λ ( T ) = c 2k T λ {\displaystyle4 B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}} .

V prípade žiarenia s dlhou vlnovou dĺžkou výsledky predpovedané touto rovnicou dobre zodpovedali praktickým výsledkom získaným v laboratóriu. Avšak v prípade krátkych vlnových dĺžok (ultrafialové žiarenie) bol rozdiel medzi teóriou a praxou taký veľký, že si vyslúžil prezývku "ultrafialová katastrofa".

Planckov zákon

v roku 1895 Wien publikoval výsledky svojich štúdií o žiarení čierneho telesa. Jeho vzorec bol:

B λ ( T ) = h 2c λ 2e5 - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Tento vzorec fungoval dobre pre elektromagnetické žiarenie s krátkou vlnovou dĺžkou, ale nefungoval dobre pre dlhé vlnové dĺžky.

V roku 1900 Max Planck uverejnil výsledky svojich štúdií. Pokúsil sa vytvoriť výraz pre žiarenie čierneho telesa vyjadrené vlnovou dĺžkou, pričom predpokladal, že žiarenie pozostáva z malých kvánt, a potom sa snažil zistiť, čo sa stane, ak sa tieto kvantá stanú nekonečne malými. (Ide o štandardný matematický prístup). Výraz bol nasledovný:

B λ ( T ) = h 2c λ2 e51 h c λ k T - 1{\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}} .

Ak sa umožní, aby vlnová dĺžka svetla bola veľmi veľká, potom možno ukázať, že Raleighov-Jeansov a Planckov vzťah sú takmer identické.

Vypočítal h a k a zistil, že

h = 6,55 ×⁻²⁷ 10 erg-sec.

k = 1,34 ×⁻¹⁶ 10 erg-deg^-1.

Tieto hodnoty sú blízke súčasným akceptovaným hodnotám 6,62606×10⁻³⁴ a 1,38065×10⁻¹⁶. Planckov zákon sa dobre zhoduje s experimentálnymi údajmi, ale jeho plný význam bol docenený až o niekoľko rokov neskôr.

Kvantová teória svetla

Ukázalo sa, že elektróny sú fotoelektrickým efektom vytláčané, ak svetlo dosiahne hraničnú frekvenciu. Pod touto hodnotou sa z kovu nemôžu uvoľniť žiadne elektróny. V roku 1905 Albert Einstein uverejnil článok, v ktorom tento efekt vysvetlil. Einstein navrhol, že svetelný lúč nie je vlna šíriaca sa priestorom, ale skôr súbor diskrétnych vlnových paketov (fotónov), z ktorých každý má energiu. Einstein uviedol, že tento efekt je spôsobený nárazom fotónu do elektrónu. To dokazuje časticovú povahu svetla.

Einstein tiež zistil, že elektromagnetické žiarenie s veľkou vlnovou dĺžkou nemá žiadny účinok. Podľa Einsteina to bolo preto, lebo "častice" nemali dostatočnú energiu na to, aby narušili elektróny.

Plank navrhol, že energia každého fotónu súvisí s frekvenciou fotónu pomocou Planckovej konštanty. Matematicky by sa to dalo zapísať takto:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}} .

Plank dostal Nobelovu cenu v roku 1918 za zásluhy o rozvoj fyziky, ktoré preukázal objavom energetických kvánt. V roku 1921 dostal Einstein Nobelovu cenu za spojenie Planckovej konštanty s fotoelektrickým efektom.

Ilustrácia prevzatá z pôvodného Newtonovho listu Kráľovskej spoločnosti (1. januára 1671 [juliánsky kalendár]). S predstavuje slnečné svetlo. Svetlo medzi rovinami BC a DE je farebné. Tieto farby sa rekombinujú a vytvárajú slnečné svetlo na rovine GH


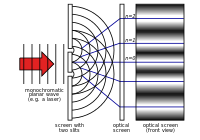
Youngov dvojštrbinový experiment


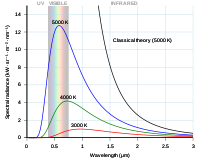
Rayleighova-Jeansova krivka a Planckova krivka vykreslené v závislosti od vlnovej dĺžky fotónu.


Konferencia Solway 1911. Planck, Einstein a Jeans stoja. Planck je druhý zľava. Einstein je druhý sprava. Jeans je piaty sprava. Wien sedí, tretí sprava

Aplikácia

Planckova konštanta má význam v mnohých aplikáciách. Niektoré z nich sú uvedené nižšie.

Bohrov model atómu

V roku 1913 Niels Bohr uverejnil Bohrov model štruktúry atómu. Bohr povedal, že uhlový moment elektrónov obiehajúcich okolo jadra môže mať len určité hodnoty. Tieto hodnoty sú dané rovnicou

L = n h π 2{\displaystyle L=n{\frac {h}{2\pi }}}

kde

L = uhlový moment spojený s hladinou.

n = celé kladné číslo.

h = Planckova konštanta.

Na výpočet energie elektrónov na jednotlivých hladinách možno použiť Bohrov model atómu. Elektróny zvyčajne vypĺňajú najnižšie očíslované stavy atómu. Ak atóm dostane energiu napríklad od elektrického prúdu, elektróny sa excitujú do vyššieho stavu. Elektróny potom klesnú späť do nižšieho stavu a stratia svoju dodatočnú energiu vyžiarením fotónu. Keďže energetické hladiny majú špecifické hodnoty, fotóny budú mať špecifické energetické hladiny. Takto vyžiarené svetlo možno pomocou hranola rozdeliť na rôzne farby. Každý prvok má svoj vlastný vzor. Vzor neónu je znázornený vedľa.

Heisenbergov princíp neurčitosti

V roku 1927 Werner Heisenberg zverejnil princíp neurčitosti. Tento princíp hovorí, že nie je možné vykonať meranie bez toho, aby sa narušila meraná vec. Stanovuje tiež hranicu minimálneho narušenia spôsobeného meraním.

V makroskopickom svete sú tieto poruchy veľmi malé. Ak sa napríklad meria teplota banky s kvapalinou, teplomer pri zahrievaní absorbuje malé množstvo energie. To spôsobí malú chybu v konečnom údaji, ale táto chyba je malá a nie je dôležitá.

V kvantovej mechanike je to inak. Niektoré merania sa vykonávajú na základe vzorca rozptýlených fotónov. Jedným z takýchto príkladov je Comptonov rozptyl. Ak sa meria poloha aj hybnosť častice, princíp neurčitosti hovorí, že existuje kompromis medzi presnosťou, s akou sa meria hybnosť, a presnosťou, s akou sa meria poloha. Rovnica, ktorá opisuje tento kompromis, je:

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad }

kde

Δp = neistota hybnosti.

Δx = neistota polohy.

h = Planckova konštanta.

Farba svetelných diód

V elektrickom obvode znázornenom vpravo závisí úbytok napätia na svetelnej dióde (LED) od materiálu LED. V prípade kremíkových diód je tento úbytok 0,6 V. V prípade LED diód sa však pohybuje medzi 1,8 V a 2,7 V. Táto informácia umožňuje používateľovi vypočítať Planckovu konštantu.

Energia potrebná na preskočenie potenciálnej bariéry jedným elektrónom v materiáli LED je daná vzťahom

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

kde

Q_e je náboj jedného elektrónu.

V_L je úbytok napätia na LED.

Keď sa elektrón opäť rozpadne, vyžiari jeden fotón svetla. Energia fotónu je daná tou istou rovnicou, ktorá sa používa pri fotoelektrickom efekte. Ak sa tieto rovnice skombinujú, vlnová dĺžka svetla a napätie súvisia

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}},}

Z tohto vzťahu možno vypočítať nasledujúcu tabuľku.

Farba	Vlnová dĺžka (nm)	Napätie
červené svetlo	650	1.89
zelené svetlo	550	2.25
modré svetlo	470	2.62

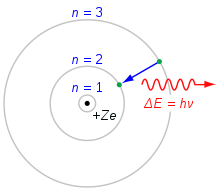
Bohrov model atómu. Elektrón padajúci z obalu n=3 do obalu n=2 stráca energiu. Táto energia sa prenáša ako jeden fotón.


Viditeľné spektrum neónu. Každá čiara predstavuje iný pár energetických hladín.


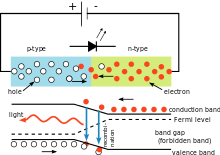
Jednoduchý LED obvod, ktorý ilustruje použitie Planckovej konštanty. Farba vyžarovaného svetla závisí od úbytku napätia na dióde. Vlnová dĺžka svetla sa dá vypočítať pomocou Planckovej konštanty.

Hodnota Planckovej konštanty a nová definícia kilogramu

Od jeho objavu sa meranie h výrazne zlepšilo. Planck prvýkrát uviedol hodnotu h 6,55 × 10 ⁻²⁷erg-sec. Táto hodnota je v rozmedzí 5 % od súčasnej hodnoty.

K 3. marcu 2014 je najlepšia nameraná hodnota h v jednotkách SI 6,62606957 ×⁻³⁴ 10 J-s. Ekvivalentná hodnota v jednotkách cgs je 6,62606957×10 ⁻²⁷erg-sec. Relatívna neistota h je 4,4×10⁻⁸.

Redukovaná Planckova konštanta (ħ) je hodnota, ktorá sa niekedy používa v kvantovej mechanike. Je definovaná ako

ℏ = h π 2{\displaystyle \hbar ={\frac {h}{2\pi }}} .

V kvantovej mechanike sa niekedy namiesto SI používajú Planckove jednotky. V tejto sústave má redukovaná Planckova konštanta hodnotu 1, takže hodnota Planckovej konštanty je 2π.

Plancksovu konštantu možno teraz merať s veľmi vysokou presnosťou. To viedlo BIPM k tomu, aby zvážila novú definíciu kilogramu. Na definovanie kilogramu sa už nepoužíva medzinárodný prototyp kilogramu. Namiesto toho BIPM definuje Planckovu konštantu tak, aby mala presnú hodnotu. Vedci používajú túto hodnotu a definície metra a sekundy na definovanie kilogramu.

 

Hodnota teoretickej Planckovej konštanty

Planckovu konštantu možno odvodiť aj matematicky:

 

h = μ π0 c12 [ 3q [ 0a0.9163 ]0 ] 2f2 r 15⋅ s = ×6.6310 - 34J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}}{[0,9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}\cdot {s}=6,63\times 10^{-34}J\cdot s}

Tu μ {\displaystyle0 \mu _{0}} je permeabilita voľného priestoru, c {\displaystyle c} je rýchlosť svetla, q {\displaystyle0 q_{0}} je elektrický náboj elektrónu, a {\displaystyle0 a_{0}} je Bohrov polomer a f r 1{\displaystyle f_{1r}} je frekvencia otáčania elektrónu v atóme vodíka ( f r 1= ×3.29 r1015 e v / s ) {\displaystyle (f_{1r}=3.29\times 10^{15}rev/s)} . Keď sa tieto hodnoty konštánt dosadia do teoretickej Planckovej konštanty, teoretická hodnota Planckovej konštanty sa presne rovná experimentálnej hodnote.

Súvisiace stránky

• Dualizmus vlny a častice