Fourierova transformácia

Fourierova transformácia je matematická funkcia, ktorú možno použiť na zistenie základných frekvencií, z ktorých sa skladá signál alebo vlna. Ak sa napríklad hrá akord, zvukovú vlnu akordu možno vložiť do Fourierovej transformácie a nájsť noty, z ktorých sa akord skladá. Výstup Fourierovej transformácie sa niekedy nazýva frekvenčné spektrum alebo rozdelenie, pretože zobrazuje spektrum frekvencií vstupu. Táto funkcia má mnoho využití v kryptografii, oceánografii, strojovom učení, rádiológii, kvantovej fyzike, ako aj v dizajne a vizualizácii zvuku.

Fourierova transformácia funkcie f ( x ) {\displaystyle f(x)} f(x) je daná vzťahom

F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx} $F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx$

α {\displaystyle \alpha } $\alpha$ je frekvencia

F ( α ) {\displaystyle F(\alpha )} $F(\alpha )$ je funkcia Fourierovej transformácie a vracia hodnotu vyjadrujúcu, ako prevláda frekvencia α {\displaystyle \alpha } $\alpha$ v pôvodnom signále.

e - 2 π i α x {\displaystyle e^{-2\pi i\alfa x}} $e^{-2\pi i\alpha x}$ Predstavuje obtekanie vstupnej funkcie f ( x ) {\displaystyle f(x)} f(x) okolo počiatku v komplexnej rovine pri určitej frekvencii α {\displaystyle \alpha } $\alpha$

Inverzná Fourierova transformácia je daná vzťahom

f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha } $f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha$

Fourierova transformácia ukazuje, aké frekvencie sa nachádzajú v signáli. Uvažujme napríklad zvukovú vlnu, ktorá obsahuje tri rôzne hudobné tóny: Zhotovenie grafu Fourierovej transformácie tejto zvukovej vlny (s frekvenciou na osi x a intenzitou na osi y) ukáže vrchol na každej frekvencii, ktorý zodpovedá jednej z hudobných nôt.

Sčítaním kosínusov a sínusov s rôznymi amplitúdami a frekvenciami možno vytvoriť mnoho signálov. Fourierova transformácia zobrazuje amplitúdy a fázy týchto kosínusov a sínusov v závislosti od ich príslušných frekvencií.

Fourierove transformácie sú dôležité, pretože mnohé signály majú väčší zmysel, keď sú ich frekvencie oddelené. V uvedenom príklade zvuku pri pohľade na signál vzhľadom na čas nie je zrejmé, že v signále sú tóny A, B a C. Mnohé systémy robia rôzne veci s rôznymi frekvenciami, takže tieto druhy systémov možno opísať podľa toho, čo robia s jednotlivými frekvenciami. Príkladom je filter, ktorý blokuje vysoké frekvencie.

Výpočet Fourierovej transformácie si vyžaduje pochopenie integrácie a imaginárnych čísel. Na výpočet Fourierových transformácií sa zvyčajne používajú počítače, okrem najjednoduchších signálov. Rýchla Fourierova transformácia je metóda, ktorú počítače používajú na rýchly výpočet Fourierovej transformácie.

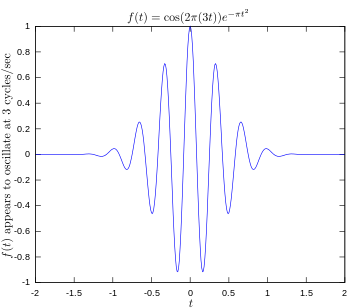
Pôvodná funkcia zobrazujúca signál kmitajúci pri frekvencii 3 hertzov.

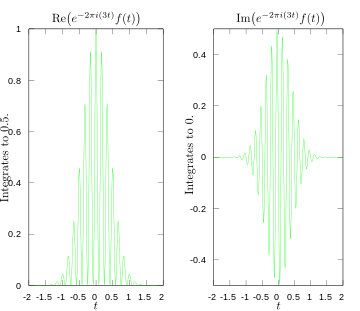
Reálne a imaginárne časti integrálu pre Fourierovu transformáciu pri frekvencii 3 Hz

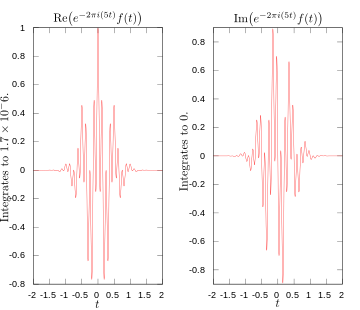
Reálne a imaginárne časti integrálu pre Fourierovu transformáciu pri frekvencii 5 hertzov

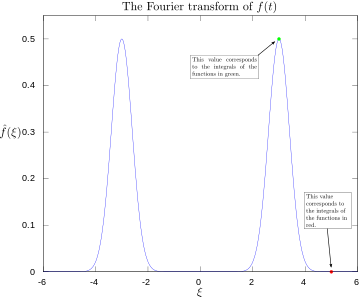
Fourierova transformácia s označením 3 a 5 hertzov.

Otázky a odpovede

Otázka: Čo je to Fourierova transformácia?

Odpoveď: Fourierova transformácia je matematická funkcia, ktorá sa dá použiť na zistenie základných frekvencií, z ktorých sa skladá vlna. Vezme komplexnú vlnu a nájde frekvencie, ktoré ju tvoria, čo umožňuje identifikovať tóny, ktoré tvoria akord.

Otázka: Aké sú niektoré spôsoby použitia Fourierovej transformácie?

Odpoveď: Fourierova transformácia má mnoho využití v kryptografii, oceánografii, strojovom učení, rádiológii, kvantovej fyzike, ako aj v dizajne a vizualizácii zvuku.

Otázka: Ako sa vypočíta Fourierova transformácia?

Odpoveď: Fourierova transformácia funkcie f(x) je daná vzťahom F(ב) = ∫-∞+∞f(x)e-2נiבxdx, kde ב je frekvencia. Vráti sa hodnota vyjadrujúca, ako prevláda frekvencia ב v pôvodnom signáli. Inverzná Fourierova transformácia je daná vzťahom f(x) = ∫-∞+∞F(ב)e+2נixבdב.

Otázka: Ako vyzerá výstup Fourierovej transformácie?

Odpoveď: Výstup Fourierovej transformácie možno nazvať buď frekvenčným spektrom, alebo rozdelením, pretože zobrazuje rozdelenie možných frekvencií vstupu.

Otázka: Ako počítače počítajú rýchle Fourierove transformácie?

Odpoveď: Počítače používajú algoritmus nazývaný Rýchla Fourierova transformácia (FFT) na rýchly výpočet akejkoľvek transformácie signálu okrem tých najjednoduchších.

Otázka: Čo nám neukazuje pohľad na signály vzhľadom na čas?

Odpoveď: Pri pohľade na signály vzhľadom na čas nie je zrejmé, aké tóny sú v nich prítomné; mnohé signály dávajú väčší zmysel, keď sa ich frekvencie oddelia a analyzujú jednotlivo.