Vektor (matematika)

Príklady vektorov

• John prejde 20 metrov na sever. Smer "sever" spolu so vzdialenosťou "20 metrov" je vektor.
• Jablko padá dole rýchlosťou 10 metrov za sekundu. Smer "dole" v kombinácii s rýchlosťou "10 metrov za sekundu" je vektor. Tento druh vektora sa nazýva aj rýchlosť.

Príklady skalárov

• Vzdialenosť medzi dvoma miestami je 10 kilometrov. Táto vzdialenosť nie je vektor, pretože neobsahuje smer.
• Počet ovocia v krabici nie je vektor.
• Osoba, ktorá ukazuje, nie je vektor, pretože existuje len smer. Neexistuje žiadna veľkosť (napríklad vzdialenosť od prsta osoby k budove).
• Dĺžka objektu.
• Auto jazdí rýchlosťou 100 kilometrov za hodinu. Toto nie je opis vektora, pretože je tu len veľkosť, ale nie smer.

Ďalšie príklady vektorov

• Posunutie je vektor. Posunutie je vzdialenosť, o ktorú sa niečo pohybuje určitým smerom. Samotná miera vzdialenosti je skalár.
• Sila, ktorá zahŕňa smer, je vektor.
• Rýchlosť je vektor, pretože je to rýchlosť v určitom smere.
• Zrýchlenie je miera zmeny rýchlosti. Objekt zrýchľuje, ak mení rýchlosť alebo smer.

Ako pridať vektory

Pridávanie vektorov na papier pomocou metódy head to tail

Metóda sčítania vektorov Head to Tail je užitočná na odhad výsledku sčítania dvoch vektorov na papieri. Postupuje sa takto:

• Každý vektor je nakreslený ako šípka s určitou dĺžkou, pričom každá jednotka dĺžky na papieri predstavuje určitú veľkosť vektora.
• Nakreslite ďalší vektor, pričom chvost (koniec) druhého vektora bude v hlave (čele) prvého vektora.
• Opakujte pre všetky ďalšie vektory: Nakreslite chvost ďalšieho vektora v hlave predchádzajúceho vektora.
• Nakreslite čiaru od chvosta prvého vektora k hlave posledného vektora - to je výslednica (súčet) všetkých vektorov.

Nazýva sa metóda "Head to Tail", pretože každá hlava z predchádzajúceho vektora vedie k chvostu ďalšieho vektora.

Použitie formulára komponentu

^{[je potrebné vysvetliť}

Použitie tvaru komponenta na sčítanie dvoch vektorov doslova znamená sčítanie komponentov vektorov, čím sa vytvorí nový vektor. Nech sú napríklad a a b dva dvojrozmerné vektory. Tieto vektory možno zapísať v tvare ich zložiek.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})}

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})}

Predpokladajme, že c je súčet týchto dvoch vektorov, takže c = a + b. To znamená, že c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} .

Tu je príklad sčítania dvoch vektorov pomocou ich zložiek.

a = ( ,3 -1 ) {\displaystyle \mathbf {a} =(3,-1)}

b = ( ,2 ) 2{\displaystyle \mathbf {b} =(2,2)}

c = a + b {\displaystyle \mathbf {c} =\mathbf {a} +\mathbf {b} }

= ( a x + b x , a y + b y ) {\displaystyle =(a_{x}+b_{x},a_{y}+b_{y})}

= ( +3 , 2- 1+ ) 2{\displaystyle =(3+2,-1+2)}

= ( ,5 ) 1{\displaystyle =(5,1)}

Táto metóda funguje pre všetky vektory, nielen pre dvojrozmerné.

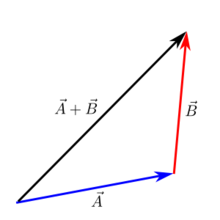
Doplnenie Head-to-tail

Ako násobiť vektory

Použitie bodového súčinu

Bodový súčin je jednou z metód násobenia vektorov. Jeho výsledkom je skalár. Používa tvar komponentu:

a = ( ,2 ) 3b = ( ,1 ) 4a ⋅ b = ( ,2 ) 3⋅ ( ,1 ) 4= ( 2⋅1 ) + ( 3⋅4 ) = +2 = 12{\displaystyle14 {\begin{aligned}\mathbf {a} =(2,3)\\\mathbf {b} =(1,4)\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\=(2\cdot 1)+(3\cdot 4)\\=2+12=14\end{aligned}}

Použitie krížového súčinu

Krížový súčin je ďalšia metóda násobenia vektorov. Jeho výsledkom je ďalší vektor. Použitie tvaru komponentu:

a × b = | a | | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n} }

Tu | a | {\displaystyle |\mathbf {a} |} znamená dĺžku {\displaystyle \mathbf {a} } a n {\displaystyle \mathbf {n} } je jednotkový vektor kolmý na a {\displaystyle \mathbf {a} } a b {\displaystyle \mathbf {b} } .

Násobenie skalárom

Ak chcete vynásobiť vektor skalárom (normálnym číslom), vynásobte toto číslo každou zložkou vektora:

c x = ( c x , 1c x , 2. . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})}

Príkladom je

c = x5 = ( ,3 ) 4c x = ( 5⋅3 , 5⋅4 ) = ( ,15 ) 20{\displaystyle {\begin{aligned}c=5\\\mathbf {x} =(3,4)\\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\=(15,20)\end{aligned}}}

Súvisiace stránky

• Vektorová grafika
• Vektorové pole