Pí (π) — matematická konštanta: definícia, hodnota a vlastnosti
Pí (π) — detailný prehľad matematickej konštanty: definícia, presná hodnota, iracionálne vlastnosti, použitia a zaujímavosti o nekonečnom desiatkovom rozvoji.
Pí (alebo π) je matematická konštanta. Je to pomer vzdialenosti okolo kruhu k jeho priemeru. Výsledkom je číslo, ktoré je vždy rovnaké. Toto číslo je však dosť zvláštne. Číslo začína ako 3,141592653589793... a pokračuje bez konca. Takéto čísla sa nazývajú iracionálne čísla.
Priemer je najväčšia šnúra, ktorá sa zmestí do kruhu. Prechádza stredom kružnice. Vzdialenosť okolo kruhu sa nazýva obvod. Aj keď priemer a obvod sú pre rôzne kružnice rôzne, číslo pí zostáva konštantné: jeho hodnota sa nikdy nemení. Je to preto, že vzťah medzi obvodom a priemerom je vždy rovnaký.
Základné vzťahy
Najčastejšie používané vzťahy s pí sú:
- Obvod kruhu: C = π·d = 2·π·r, kde d je priemer a r polomer.
- Plocha kruhu: A = π·r².
Pí sa objavuje aj v mnohých ďalších vzorcoch matematiky, fyziky a inžinierstva — napríklad v trigonometrických funkciách, Fourierovej analýze, geometrii a v riešení diferenciálnych rovníc.
Hodnota a aproximácie
Najvýraznejšou vlastnosťou pí je, že jeho desatinné rozvinutie nemá koniec ani pravidelný opakujúci sa vzor. Bežne používané aproximácie sú 3,14, zlomok 22/7 (približne 3,142857...), alebo presnejší 355/113 (približne 3,14159292). Pre numerické výpočty sa používajú špecializované algoritmy, ktoré dávajú zhodu na stovky, tisíce či viac desatinných miest.
V moderných počítačoch sú vypočítané miliardy až bilióny (10^9 – 10^12 a viac) desatinných miest pí; počet známych číslic sa neustále zvyšuje vďaka rýchlym algoritmom a výpočtovým výkonu.
Matematické vlastnosti
- Iracionalita: Pí nie je zlomok dvoch celých čísel. Prvá formálna dôkaz tejto skutočnosti pochádza z 18. storočia.
- Transcendencia: Pí nie je riešením žiadnej nenulovej polynomiálnej rovnice s celočíselnými koeficientmi. Túto vlastnosť dokázal Ferdinand von Lindemann v roku 1882, čo malo za následok napr. nemožnosť presne "zostrojiť" kruh so štvorcom pomocou pravítka a kružidla (tzv. problém kvadrácie kruhu).
- Výskyt v analýze: Pí sa vyskytuje v nekonečných radách (napr. Leibnizov vzťah π/4 = 1 − 1/3 + 1/5 − 1/7 + ...), v integráloch a v komplexnej analýze (napr. Eulerova identita e^{iπ} + 1 = 0 spája základné matematické konštanty).
Krátka história a výpočet
Poznanie pomeru obvodu a priemeru má veľmi dlhú históriu. Už staroveké civilizácie (Babylončania, Egypťania) používali hrubé aproximácie. Archimedes z Syrakúz v 3. storočí pred n. l. použil metódu vkladaných pravidelných mnohouholníkov a určil interval, v ktorom sa pí nachádza. Neskôr prispeli k presnosti matematickí a astronomickí školáci v rôznych kultúrach (Čína, India, islamský svet).
Súčasné výpočty používajú rýchle sériové a numerické metódy (Machinove a Machinove typy vzorcov, Gauss–Legendreho metóda, Chudnovského algoritmus a ďalšie), ktoré umožňujú získať obrovský počet desatinných miest.
Použitie v praxi
Pí sa nachádza v mnohých praktických oblastiach: meranie a konštrukcia kruhov a valcov, signálové spracovanie (Fourierova analýza), kvantová mechanika, teória pravdepodobnosti a štatistika (napríklad v normálnom rozdelení), spracovanie obrazu, inžinierstvo a ďalšie.
Pí je teda univerzálna konštanta, ktorá spája jednoduchú geometriu kruhu s hlbokými oblasťami modernej matematiky a vedy.
π = C d {\displaystyle \pi ={\frac {C}{d}}} 
(pí sa rovná obvodu delenému priemerom).
Pí je nekonečný rad čísel
Aproximácia
Pí sa často zapisuje formálne ako π alebo grécke písmeno π ako skratka. Pí je tiež iracionálne číslo, čo znamená, že sa nedá zapísať ako zlomok ( a b {\displaystyle a \over b}
), kde "a" a "b" sú celé čísla (celé čísla). To v podstate znamená, že číslice čísla pí, ktoré sú napravo od desatinného čísla, sa do nekonečna neopakujú v nejakom vzorci a že presnú hodnotu čísla pí nie je možné zapísať ako číslo. Pí sa dá len približne určiť alebo zmerať na hodnotu, ktorá je dostatočne blízka na praktické účely.
Hodnota blízka pí je 3,141592653589793238462643... Bežná aproximácia zlomku pí je 22 7 {\displaystyle 22 \over 7} 
, čo dáva približne 3,14285714. Táto aproximácia je vzdialená od skutočnej hodnoty pí o 0,04 %. Zatiaľ čo táto aproximácia je akceptovaná pre väčšinu jej použitia v reálnom živote, zlomok 355 113 {\displaystyle 355 \over 113}
je presnejší (dáva približne 3,14159292) a môže sa použiť, keď je potrebná hodnota bližšia k pí. Na získanie lepšej aproximácie čísla pí možno použiť počítače.
V marci 2019 Emma Haruka Iwao vypočítala hodnotu čísla pí na 31,4 bilióna číslic.
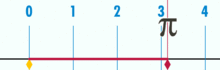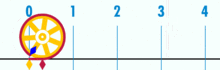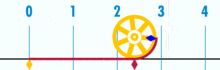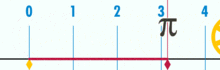
Diagram znázorňujúci, ako sa dá π nájsť pomocou kružnice s priemerom jedna. Obvod tohto kruhu je π.
História
Hodnotu pí poznali už staroindickí matematici ako Bhaskaracharya a Aryabhatta.
Matematici vedia o čísle pí už tisícky rokov, pretože rovnako dlho pracujú s kružnicami. Už civilizácie staré ako Babylončania dokázali priblížiť hodnotu pí na mnoho číslic, napríklad na zlomok 25/8 a 256/81. Väčšina historikov sa domnieva, že starí Egypťania nemali pojem π a že táto zhoda je náhodná.
Prvá písomná zmienka o čísle pí pochádza z roku 1900 pred Kristom. Okolo roku 1650 pred n. l. uviedol egyptský Ahmes hodnotu v papyruse Rhind. Babylončania dokázali zistiť, že hodnota pí je o niečo väčšia ako 3, a to tak, že jednoducho urobili veľký kruh a potom na jeho obvod a priemer prilepili kúsok lana, zaznamenali ich vzdialenosti a potom obvod vydelili priemerom.
Znalosť čísla pí sa dostala späť do Európy a do rúk Hebrejov, ktorí toto číslo zaradili do časti Biblie nazývanej Starý zákon. Potom najbežnejším spôsobom, ako sa pokúsiť nájsť číslo pí, bolo nakresliť útvar s mnohými stranami vnútri ľubovoľného kruhu a pomocou plochy útvaru nájsť číslo pí. Grécky filozof Archimedes napríklad použil na nájdenie hodnoty pí tvar mnohouholníka, ktorý mal 96 strán, ale Číňania v roku 500 n. l. dokázali na nájdenie hodnoty pí použiť mnohouholník so 16 384 stranami. Gréci, ako napríklad Anaxagoras z Klazoménie, sa zaoberali aj zisťovaním ďalších vlastností kruhu, napríklad ako z kružníc vytvoriť štvorce a odmocniť číslo pí. Odvtedy sa mnohí ľudia snažili zistiť čoraz presnejšie hodnoty čísla pí.
| História pí | ||
| Filozof | Dátum | Aproximácia |
| okolo roku 150 n. l. | 3.1416 | |
| Zu Chongzhi | 430-501 N. L. | 3.1415929203 |
| al-Khwarizmi | okolo roku 800 n. l. | 3.1416 |
| al-Kashi | okolo roku 1430 | 3.14159265358979 |
| Viète | 1540-1603 | 3.141592654 |
| Roomen | 1561-1615 | 3.14159265358979323 |
| Van Ceulen | okolo roku 1600 | 3.14159265358979323846264338327950288 |
V 16. storočí boli k dispozícii stále lepšie spôsoby, ako nájsť číslo pí, napríklad zložitý vzorec, ktorý vyvinul francúzsky právnik François Viète. Prvýkrát bol grécky symbol "π" použitý v eseji Williama Jonesa z roku 1706.
Matematik Lambert v roku 1761 tiež dokázal, že číslo pí je iracionálne, to znamená, že sa nedá zapísať ako zlomok podľa bežných noriem. Ďalší matematik menom Lindeman dokázal v roku 1882, že pí patrí do skupiny čísel známych ako transcendentné čísla, čo sú čísla, ktoré nemôžu byť riešením polynomickej rovnice.
Pí sa dá použiť aj na určenie mnohých iných vecí okrem kružníc. Vlastnosti čísla pí umožnili jeho využitie v mnohých ďalších oblastiach matematiky okrem geometrie, ktorá skúma tvary. Niektoré z týchto oblastí sú komplexná analýza, trigonometria a rady.
Pi v reálnom živote
Dnes existujú rôzne spôsoby výpočtu mnohých číslic čísla π. Má to však obmedzený význam.
Pí sa niekedy používa na určenie plochy alebo obvodu ľubovoľného kruhu. Ak chcete zistiť obvod kruhu, použite vzorec C (obvod) = π krát priemer. Ak chcete zistiť plochu kruhu, použite vzorec π (polomer²). Tento vzorec sa niekedy zapisuje ako A = π r 2 {\displaystyle A=\pi r^{2}} 
, kde r je premenná pre polomer ľubovoľnej kružnice a A je premenná pre plochu tejto kružnice.
Výpočet obvodu kruhu s chybou 1 mm:
- Pre polomer 30 metrov sú potrebné 4 číslice
- 10 číslic pre polomer rovný polomeru Zeme
- 15 číslic pre polomer rovnajúci sa vzdialenosti Zeme od Slnka.
Ľudia zvyčajne oslavujú 14. marec ako Deň pí, pretože 14. marec sa píše aj ako 3/14, čo predstavuje prvé tri čísla 3,14 v aproximácii čísla pí. Deň pí sa začal sláviť v roku 2001.
Súvisiace stránky
Otázky a odpovede
Otázka: Aké je číslo ً?
Odpoveď: ً je matematická konštanta, ktorá je pomerom obvodu kruhu k jeho priemeru.
Otázka: Čo z toho vyplýva?
Odpoveď: Výsledkom je číslo, ktoré je vždy rovnaké.
Otázka: Ako toto číslo začína?
Odpoveď: Číslo začína ako 3,141592653589793... a pokračuje bez konca.
Otázka: O aký typ čísla ide?
Odpoveď: Tieto čísla sa nazývajú iracionálne čísla.
Otázka: Aký je priemer kruhu?
Odpoveď: Priemer kruhu je najväčšia tetiva, ktorá sa do neho zmestí a prechádza jeho stredom.
Otázka: Čo je to obvod kruhu? Odpoveď: Vzdialenosť okolo kruhu sa nazýva obvod.
Otázka: Zostáva číslo pí konštantné bez ohľadu na rôzne kružnice? Odpoveď: Áno, pí zostáva konštantné bez ohľadu na rôzne kružnice, pretože vzťah medzi ich obvodom a priemerom zostáva vždy rovnaký.
Prehľadať