Bodový súčin

V matematike je bodový súčin operácia, ktorá ako vstup berie dva vektory a ako výstup vracia skalárne číslo. Vrátené číslo závisí od dĺžky oboch vektorov a od uhla medzi nimi. Názov je odvodený od stredovej bodky "-", ktorá sa často používa na označenie tejto operácie; alternatívny názov skalárny súčin zdôrazňuje skalárny (a nie vektorový) charakter výsledku.

Bodový súčin je v kontraste (v trojrozmernom priestore) s krížovým súčinom, ktorého výsledkom je vektor.

Definícia

Bodový súčin dvoch vektorov a = [a₁ , a₂ , ..., a_n ] a b = [b₁ , b₂ , ..., b_n ] je definovaný ako:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}} $\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

kde Σ označuje súčtový zápis (súčet všetkých členov) a n je dimenzia vektorového priestoru.

V dimenzii 2 je bodový súčin vektorov [a,b] a [c,d] ac + bd. Rovnako v dimenzii 3 je bodový súčin vektorov [a,b,c] a [d,e,f] ad + be + cf. Napríklad bodový súčin dvoch trojrozmerných vektorov [1, 3, -5] a [4, -2, -1] je

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.} $[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

Geometrická interpretácia

V euklidovskej geometrii spolu súvisia bodový súčin, dĺžka a uhol. Pre vektor a je bodový súčin a - a štvorcom dĺžky a alebo

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}} ${\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}$

kde ||a|| označuje dĺžku (veľkosť) a. Všeobecnejšie, ak b je iný vektor

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \pravý\|\cos \theta \,} $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,$

kde ||a|| a ||b| označujú dĺžky a a b a θ je uhol medzi nimi.

Tento vzorec možno preusporiadať tak, aby sa určila veľkosť uhla medzi dvoma nenulovými vektormi:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)} $\theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)$

Vektory možno tiež najprv previesť na jednotkové vektory vydelením ich magnitúdou:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}} ${\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}$

potom uhol θ je daný vzťahom

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})} $\theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})$

Keďže kosínus 90° je nulový, bodový súčin dvoch kolmých vektorov je vždy nulový. Okrem toho dva vektory možno považovať za ortogonálne vtedy a len vtedy, ak je ich bodový súčin nulový a oba majú nenulovú dĺžku. Táto vlastnosť poskytuje jednoduchú metódu na testovanie podmienky ortogonality.

Niekedy sa tieto vlastnosti používajú aj na definovanie bodového súčinu, najmä v 2 a 3 rozmeroch; táto definícia je ekvivalentná s vyššie uvedenou. Pre vyššie rozmery možno vzorec použiť na definovanie pojmu uhla.

Geometrické vlastnosti závisia od toho, či je báza ortonormálna, t. j. či sa skladá z dvojíc na seba kolmých vektorov s jednotkovou dĺžkou.

Skalárna projekcia

Ak majú a aj b dĺžku jedna (t. j. sú to jednotkové vektory), ich bodový súčin jednoducho udáva kosínus uhla medzi nimi.

Ak je len b jednotkový vektor, potom bodový súčin a - b dáva |a| cos(θ), t. j. veľkosť priemetu a do smeru b, so znamienkom mínus, ak je smer opačný. Toto sa nazýva skalárna projekcia a na b alebo skalárna zložka a v smere b (pozri obrázok). Táto vlastnosť bodového súčinu má niekoľko užitočných aplikácií (pozri napríklad nasledujúcu časť).

Ak a ani b nie je jednotkový vektor, potom veľkosť priemetu a v smere b bude napríklad a - (b / |b|), pretože jednotkový vektor v smere b je b / |b|.

Rotácia

Rotáciu ortonormálnej bázy, v ktorej je reprezentovaný vektor a, získame vynásobením a maticou rotácie R. Toto maticové násobenie je len kompaktnou reprezentáciou postupnosti bodových súčinov.

Nechajte napríklad

B₁ = {x, y, z} a B₂ = {u, v, w} sú dve rôzne ortonormálne bázy toho istého priestoru R³ , pričom B₂ získame jednoduchým otočením B₁ ,
a₁ = (a_x , a_y , a_z ) predstavujú vektor a v zmysle B₁ ,
a₂ = (a_u , a_v , a_w ) predstavujú ten istý vektor v zmysle pootočeného základu B₂ ,
u₁ , v₁ , w₁ sú pootočené bázové vektory u, v, w reprezentované v termínoch B₁ .

Potom sa vykoná rotácia z B₁ na B₂ takto:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\a_{v}\a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

Všimnite si, že rotačná matica R je zostavená pomocou rotovaných bázových vektorov u₁ , v₁ , w₁ ako jej riadkov a tieto vektory sú jednotkové vektory. Podľa definície sa Ra₁ skladá z postupnosti bodových súčinov medzi každým z troch riadkov R a vektorom a₁ . Každý z týchto bodových súčinov určuje skalárnu zložku a v smere rotovaného bázového vektora (pozri predchádzajúcu časť).

Ak je₁ riadkovým vektorom, a nie stĺpcovým vektorom, potom R musí obsahovať pootočené bázové vektory vo svojich stĺpcoch a musí sa dodatočne vynásobiť a₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\koniec{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

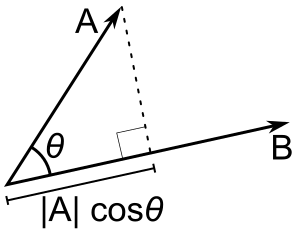
A - B = |A| |B| cos(θ). |A| cos(θ) je skalárna projekcia A na B.

Fyzika

Vo fyzike je magnitúda skalár vo fyzikálnom zmysle, t. j. fyzikálna veličina nezávislá od súradnicového systému, vyjadrená ako súčin číselnej hodnoty a fyzikálnej jednotky, nie len ako číslo. Bodový súčin je tiež skalár v tomto zmysle, daný vzorcom, nezávislý od súradnicového systému. Príklad:

Mechanická práca je bodový súčin vektorov sily a posunutia.
Magnetický tok je bodový súčin magnetického poľa a plošných vektorov.
Objemový prietok je bodový súčin rýchlosti kvapaliny a plošných vektorov.

Vlastnosti

Ak sú a, b a c reálne vektory a r je skalár, platia nasledujúce vlastnosti.

Bodový súčin je komutatívny:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . } $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$

Bodový súčin je distribučný nad vektorovým sčítaním:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . } $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

Bodový súčin je bilineárny:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). } $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

Pri násobení skalárnou hodnotou bodový súčin spĺňa:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(tieto dve posledné vlastnosti vyplývajú z prvých dvoch).

Dva nenulové vektory a a b sú kolmé vtedy a len vtedy, ak a - b = 0.

Na rozdiel od násobenia obyčajných čísel, pri ktorom platí, že ak ab = ac, potom sa b vždy rovná c, pokiaľ a nie je nula, bodový súčin sa neriadi zákonom anulovania:

Ak a - b = a - c a a ≠ 0, potom podľa distribučného zákona môžeme napísať: a - (b - c) = 0; vyššie uvedený výsledok hovorí, že to len znamená, že a je kolmé na (b - c), čo stále umožňuje (b - c) ≠ 0, a teda b ≠ c.

Ak je báza ortonormálna, bodový súčin je invariantný pri izometrických zmenách bázy: rotáciách, odrazoch a kombináciách, pričom počiatok zostáva pevný. Uvedená geometrická interpretácia sa opiera o túto vlastnosť. Inými slovami, pre ortonormálny priestor s ľubovoľným počtom rozmerov je bodový súčin invariantný pri transformácii súradníc na základe ortogonálnej matice. To zodpovedá nasledujúcim dvom podmienkam:

Nová báza je opäť ortonormálna (t. j. je ortonormálna vyjadrená v starej báze).
Nové bázové vektory majú rovnakú dĺžku ako staré (t. j. jednotkovú dĺžku v zmysle starej bázy).

Ak a a b sú funkcie, potom derivácia a - b je a' - b + a - b'

Rozšírenie trojitého súčinu

Ide o veľmi užitočnú identitu (známu aj ako Lagrangeov vzorec), ktorá zahŕňa bodový a krížový súčin. Zapisuje sa ako

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )} $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

čo je jednoduchšie zapamätať si ako "BAC mínus CAB", pričom treba mať na pamäti, ktoré vektory sú spolu bodkované. Tento vzorec sa bežne používa na zjednodušenie vektorových výpočtov vo fyzike.

Dôkaz geometrickej interpretácie

Uvažujme prvok R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,} $\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

Opakovaným použitím Pytagorovej vety získame pre jej dĺžku |v|

| v | 2 = v 1 2 + v 2 2 + . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} $|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

Ale to je to isté ako

v ⋅ v = v 1 2 + v 2 2 + . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,} $\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

Takže sme dospeli k záveru, že ak vektor v vynásobíme bodovým súčinom so sebou samým, dostaneme dĺžku vektora vo štvorci.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,} $\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

Teraz uvažujme dva vektory a a b vychádzajúce z počiatku, ktoré sú od seba vzdialené uhlom θ. Tretí vektor c možno definovať ako

c = d e f a - b . {\displaystyle \mathbf {c} {\\stackrel {\mathrm {def} }{=}}\\ \mathbf {a} -\mathbf {b} .\,} $\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,$

a vytvorí trojuholník so stranami a, b a c. Podľa zákona kosínusov máme

| c | 2 = | a | 2 + | b | 2 - 2 | a | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Nahradením bodových súčinov za štvorcové dĺžky podľa lemy 1 dostaneme

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$ (1)

Ale keďže c ≡ a - b, máme tiež

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} $\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$ ,

ktorý sa podľa distribučného zákona rozširuje na

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$ (2)

Zlúčením dvoch rovníc c - c, (1) a (2), dostaneme

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Odčítaním a - a + b - b od oboch strán a delením -2 dostaneme

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Q.E.D.

Zovšeobecnenie

Vnútorný súčin zovšeobecňuje bodový súčin na abstraktné vektorové priestory a zvyčajne sa označuje ako ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } $\langle \mathbf {a} \,,\mathbf {b} \rangle$ . Vzhľadom na geometrickú interpretáciu bodového súčinu je norma ||a|| vektora a v takomto priestore vnútorného súčinu definovaná ako

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \\mathbf {a} \,,\mathbf {a} \rangle }} $\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

tak, že zovšeobecňuje dĺžku, a uhol θ medzi dvoma vektormi a a b podľa

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}. } $\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

Dva vektory sa považujú za ortogonálne, ak je ich vnútorný súčin rovný nule

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.} $\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

V prípade vektorov s komplexnými vstupmi by použitie danej definície bodového súčinu viedlo k úplne iným geometrickým vlastnostiam. Napríklad bodový súčin vektora so sebou samým môže byť ľubovoľné komplexné číslo a môže byť nulový bez toho, aby bol vektor nulovým vektorom; to by zase malo vážne dôsledky pre pojmy ako dĺžka a uhol. Mnohé geometrické vlastnosti sa dajú zachrániť za cenu vzdania sa symetrických a bilineárnych vlastností skalárneho súčinu, a to alternatívnym definovaním

a ⋅ b = ∑ a i b i ž {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}} $\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

kde b_i je komplexný konjugát b_i . Potom skalárny súčin ľubovoľného vektora so sebou samým je nezáporné reálne číslo a je nenulový okrem nulového vektora. Tento skalárny súčin však nie je lineárny v b (ale skôr konjugovaný lineárny) a skalárny súčin nie je ani symetrický, pretože

a ⋅ b = b ⋅ a Ž {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} $\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$ .

Tento typ skalárneho súčinu je napriek tomu dosť užitočný a vedie k pojmom hermitovskej formy a všeobecného vnútorného súčinového priestoru.

Frobeniov vnútorný súčin zovšeobecňuje bodový súčin na matice. Je definovaný ako súčet súčinov príslušných zložiek dvoch matíc rovnakej veľkosti.

Zovšeobecnenie na tenzory

Bodový súčin medzi tenzorom rádu n a tenzorom rádu m je tenzor rádu n+m-2. Bodový súčin sa vypočíta vynásobením a sčítaním cez jeden index v oboch tenzoroch. Ak A {\displaystyle \mathbf {A} } $\mathbf {A}$ a B {\displaystyle \mathbf {B} } $\mathbf {B}$ sú dva tenzory so zastúpením prvkov A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} $A_{ij\dots }^{k\ell \dots }$ a B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} $B_{mn\dots }^{p{\dots }i}$ prvky bodového súčinu A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } $\mathbf {A} \cdot \mathbf {B}$ sú dané

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}} $A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

Táto definícia sa prirodzene redukuje na štandardný vektorový bodový súčin, ak sa aplikuje na vektory, a maticové násobenie, ak sa aplikuje na matice.

Príležitostne sa na vyjadrenie násobenia a sčítania cez dva indexy používa dvojitý bodový súčin. Dvojitý bodový súčin medzi dvoma tenzormi 2. rádu je skalár.

Súvisiace stránky

Cauchyho-Schwarzova nerovnosť
Krížový produkt
Násobenie matíc
Fyzika

Otázky a odpovede

Otázka: Čo je to bodový súčin v matematike?

Odpoveď: Bodový súčin je operácia, ktorá na vstupe prijíma dva vektory a na výstupe vracia skalárne číslo.

Otázka: Od čoho závisí bodový súčin?

Odpoveď: Bodový súčin závisí od dĺžky oboch vektorov a od uhla medzi nimi.

Otázka: Prečo je názov bodového súčinu odvodený od stredovej bodky "-"?

Odpoveď: Názov je odvodený od vystredenej bodky "-", ktorá sa často používa na označenie tejto operácie.

Otázka: Aký je alternatívny názov pre bodový súčin?

Odpoveď: Alternatívny názov je skalárny súčin, ktorý zdôrazňuje skalárny (a nie vektorový) charakter výsledku.

Otázka: Aký je rozdiel medzi bodovým a krížovým súčinom v trojrozmernom priestore?

Odpoveď: Výsledkom bodového súčinu je skalárne číslo, zatiaľ čo výsledkom krížového súčinu je vektor.

Otázka: Na čo sa v matematike používa bodový súčin?

Odpoveď: Bodový súčin možno použiť na určenie, či sú dva vektory kolmé (zvierajú uhol 90 stupňov), a na premietnutie jedného vektora na druhý.

Otázka: Dá sa bodový súčin použiť vo vyšších priestoroch?

Odpoveď: Áno, bodový súčin sa dá rozšíriť na vyššie rozmerové priestory zovšeobecnením definície.