Násobenie čísel: Definícia, vlastnosti a príklady

Násobenie čísel: jasná definícia, vlastnosti (komutatívnosť, škálovanie), názorné príklady a postupy pre rýchle pochopenie a precvičenie.

Násobenie je aritmetická operácia, ktorej výsledkom je súčin dvoch (alebo viacerých) čísel. V základnom učení matematiky sa násobenie radí za sčítanie a odčítanie, preto sa často považuje za tretiu základnú aritmetickú operáciu.

Definícia a základné interpretácie

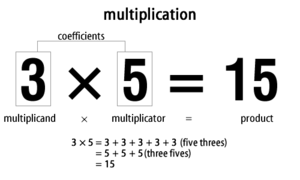
Najjednoduchšia intuícia násobenia pochádza z opakovaného sčítania: napríklad 3 × 5 znamená súčet troch päťok alebo súčet piatich trojok; výsledok je 15. Toto možno zapísať ako 3 × 5 = 15 a vysloviť "tri krát päť sa rovná pätnásť".

Pri prirodzených číslach môžeme násobenie chápať aj ako počet dielikov v mriežke (obdĺžniku), kde jedno číslo udáva počet dielikov v riadku a druhé v stĺpci. Pri reálnych číslach dávame geometrický zmysel ploche: súčin dvoch nezáporných reálnych čísel je plocha obdĺžnika s danými stranami.

Matematici často označujú čísla, ktoré násobíme, rôznymi názvami: spoločne ich niekedy nazývajú „činitele“, pričom samostatne sa stretneme s termínmi "násobiteľ" a "násobenec" (v pôvodnom texte boli použité výrazy "násobok" a "násobiteľ"). Výsledok násobenia sa nazýva súčin. Platí teda: násobiteľ × násobenec = súčin.

Geometrické a škálovacie chápanie

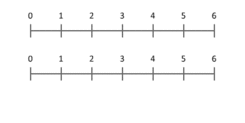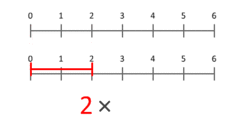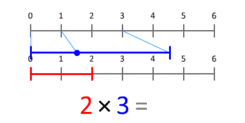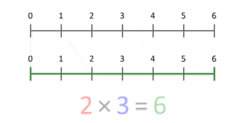
Okrem mriežky a plochy môžeme násobenie chápať ako škálovanie: násobenie čísla a reálneho parametra predstavuje zmenu veľkosti (škálu) veličiny. Napríklad, keď násobíme dĺžku 3 číslom 2, dostaneme dĺžku 6 — pôvodný úsek je zväčšený dvakrát. Toto chápanie funguje aj pre hodnoty menšie ako 1 a pre záporné čísla (záporné násobenie znamená aj otočenie smeru spolu so škálovaním).

Definícia násobenia ako opakovaného sčítania tiež poskytuje cestu k množinovo-teoretickej interpretácii násobenia kardinálnych čísel, kde súčin predstavuje karteziánsky súčin množín so zodpovedajúcim počtom prvkov.

Hlavné vlastnosti násobenia

• Komutatívnosť (pre bežné číselné množiny): poradie činiteľov nemení súčin. Pre celé čísla, racionálne čísla, reálne a komplexné čísla platí a × b = b × a.
• Asociatívnosť: (a × b) × c = a × (b × c) pre čísla v tých istých číselných oblastiach (reálne, komplexné).
• Distributívnosť voči sčítaniu: a × (b + c) = a × b + a × c. Táto vlastnosť spája násobenie so sčítaním a je základom algebraických pravidiel.
• Neutrálny element: 1 je jednotkou násobenia, pretože 1 × a = a × 1 = a pre všetky a.
• Vlastnosť nuly: 0 × a = a × 0 = 0 pre všetky a.
• Multiplikatívny inverz (pre nenulové čísla): pre každé a ≠ 0 existuje 1/a, že a × (1/a) = 1. Inverzná operácia k násobeniu je delenie.

Kedy násobenie nie je komutatívne alebo asociatívne

Hoci komutatívnosť a asociatívnosť platia pre bežné číselné polia, existujú matematické štruktúry, kde to neplatí:

• Vektory nemajú prirodzené „násobenie“ ako skalárne čísla; operácie medzi vektormi (ako skalárny súčin alebo vektorový súčin) majú špecifické vlastnosti a často nie sú komutatívne (väčšinou ale skalárne násobenie vektora je komutatívne vzhľadom na skalar).
• Matice: násobenie matíc je všeobecne nekomutatívne — A × B ≠ B × A v mnohých prípadoch.
• Kvaternióny (a ďalšie rozšírené algebraické štruktúry) sú príkladmi čísiel, kde násobenie môže byť nekomutatívne; octóny sú dokonca neasociatívne.

Príklady násobenia

• Základný príklad: 3 × 5 = 15 (opakované sčítanie: 5 + 5 + 5 = 15).
• Záporné čísla: (-2) × 4 = -8, (-2) × (-3) = 6 (dva záporné faktory dávajú kladný výsledok).
• Desatinné čísla: 1,5 × 2 = 3, 0,2 × 0,5 = 0,1.
• Zlomky: 1/2 × 3/4 = 3/8 (násobíme čitatele a menovatele).
• Komplexné čísla: (1 + 2i) × (3 + i) = 3 + i + 6i + 2i^2 = (3 - 2) + 7i = 1 + 7i.

Násobenie polí a štruktúr

Pričom násobenie v rôznych matematických štruktúrach môže mať odlišné pravidlá a interpretácie:

• Pre skaláre (reálne, racionálne, komplexné čísla) sú vlastnosti, ktoré sme spomínali, platné.
• Pri maticovom násobení ide o kombináciu riadkov a stĺpcov; poradie faktorov je dôležité.
• Pri vektoroch rozlišujeme medzi skalárnym násobením (skalár × vektor) a medzioperáciami medzi vektormi (skalárny súčin, vektorový súčin), ktoré majú svoje vlastné pravidlá.

Algoritmy násobenia a praktické pomôcky

Dôležitou zručnosťou je mechanika násobenia väčších čísel:

• Dlhé násobenie (algoritmus v stĺpcoch) pre celé čísla — rozklad na jednotky, desiatky, stovky a pod., násobenie a sčítanie či prenášanie.
• Metódy rýchleho násobenia (napr. Karatsuba, FFT pre veľmi veľké čísla) používajú sa v informatike a kryptografii.
• Násobenie desatinných čísel vyžaduje posun desatinnej čiarky podľa súčtu desatinných miest oboch činiteľov.
• Pomocou násobilky (tabuľky násobenia) sa žiaci učia základné kombinácie do 10 × 10.

Aplikácie násobenia

Násobenie sa využíva v každodennom živote i v pokročilej vede: výpočet plôch a objemov, škálovanie jednotiek, úprava cien pri viacerých kusoch, výpočty v štatistike, fyzike (napr. sila × dráha = vykonaná práca), v inžinierstve, počítačovej grafike (škálovanie vektorov), kryptografii a ďalších oblastiach.

Opakom násobenia je delenie, ktoré hľadá činiteľa, ktorý pri násobení daného čísla dá požadovaný súčin.

Zhrnutie

Násobenie je základná aritmetická operácia, ktorú možno interpretovať ako opakované sčítanie, geometrické určenie plochy alebo škálovanie. Má niekoľko kľúčových vlastností (komutatívnosť, asociatívnosť, distributívnosť), platných v bežných číselných štruktúrach, no v niektorých algebraických systémoch (matice, kvaternióny a pod.) tieto vlastnosti nemusia platiť. Poznať pravidlá násobenia a praktické algoritmy je dôležité pre každodenné výpočty aj pre vyššie matematické aplikácie.

Otázky a odpovede

Otázka: Čo je to násobenie?

Otázka: Ako sa nazývajú dve čísla, ktoré sa majú vynásobiť?

Otázka: Je násobenie komutatívne?

Otázka: Ako môžeme interpretovať násobenie kardinálnych čísel?

Otázka: Ako sa znázorňuje násobenie čísla tri číslom päť?

Otázka: Čo je opakom násobenia?

Hľadajte podľa písmena