Harmonické rady (matematika)

História

Skutočnosť, že harmonický rad sa rozchádza, prvýkrát dokázal v 14. storočí Nicole Oresme, ale zabudlo sa na to. Dôkazy podali v 17. storočí Pietro Mengoli, Johann Bernoulli a Jacob Bernoulli.

Harmonické sekvencie používajú architekti. V období baroka ich architekti používali v proporciách pôdorysov, fasád a vo vzťahoch medzi architektonickými detailmi kostolov a palácov.

Divergencia

Existuje niekoľko známych dôkazov divergencie harmonického radu. Niektoré z nich sú uvedené nižšie.

Porovnávací test

Jedným zo spôsobov, ako dokázať divergenciu, je porovnať harmonický rad s iným divergentným radom, v ktorom je každý menovateľ nahradený ďalšou najväčšou mocninou dvoch:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16}} }}}+\cdots \end{aligned}}

Každý člen harmonického radu je väčší alebo rovný príslušnému členu druhého radu, a preto súčet harmonického radu musí byť väčší alebo rovný súčtu druhého radu. Súčet druhého radu je však nekonečný:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}}pravá)+\left({\frac {1}{4}}}!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\pravo)+\levo({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\vpravo)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}

Z toho vyplýva (na základe porovnávacieho testu), že aj súčet harmonických radov musí byť nekonečný. Presnejšie, vyššie uvedené porovnanie dokazuje, že

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}

pre každé celé kladné číslo k.

Tento dôkaz, ktorý navrhol Nicole Oresme okolo roku 1350, sa považuje za vrchol stredovekej matematiky. Dodnes je štandardným dôkazom, ktorý sa vyučuje na hodinách matematiky.

Integrálny test

Je možné dokázať, že harmonický rad diverguje porovnaním jeho súčtu s nesprávnym integrálom. Uvažujme usporiadanie obdĺžnikov znázornené na obrázku vpravo. Každý obdĺžnik je široký 1 jednotku a vysoký 1/n jednotiek, takže celková plocha nekonečného počtu obdĺžnikov je súčtom harmonického radu:

plocha obdĺžnikov = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{plocha}}\\{text{obdĺžnikov}}{koniec{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

Celková plocha pod krivkou y = 1/x od 1 do nekonečna je daná divergentným nesprávnym integrálom:

plocha pod krivkou = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{oblasť pod}}\\{\text{krivka}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty . }

Keďže táto plocha je celá obsiahnutá v obdĺžnikoch, celková plocha obdĺžnikov musí byť tiež nekonečná. To dokazuje, že

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1). }

Zovšeobecnenie tohto argumentu je známe ako integrálny test.

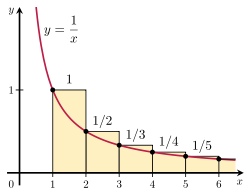
Ilustrácia integrálneho testu.

Miera divergencie

Harmonický rad sa rozchádza veľmi pomaly. Napríklad súčet prvých 1043 členov je menší ako 100. Je to preto, že čiastkové súčty radu majú logaritmický rast. Konkrétne,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}

kde γ je Eulerova-Mascheroniho konštanta a εk ~ 1/2k, ktorá sa s rastúcim k blíži k nule. Leonhard Euler to dokázal a tiež dokázal, že súčet, ktorý zahŕňa len reciproké čísla prvočísel, tiež diverguje, t. j:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty . }

Čiastkové sumy

Prvých tridsať harmonických čísel
n	Čiastkový súčet harmonického radu, Hn
	vyjadrené ako zlomok		desatinné číslo	relatívna veľkosť
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Konečné čiastkové sumy divergujúcich harmonických radov,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},}

sa nazývajú harmonické čísla.

Rozdiel medzi Hn a ln n konverguje k Eulerovej-Mascheroniho konštante. Rozdiel medzi ľubovoľnými dvoma harmonickými číslami nie je nikdy celé číslo. Žiadne harmonické čísla nie sú celé čísla, okrem _H1 = 1.

Súvisiace série

Striedavé harmonické rady

Séria

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }

je známy ako striedavý harmonický rad. Tento rad konverguje pomocou testu striedavého radu. Najmä súčet sa rovná prirodzenému logaritmu 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.}

Striedavý harmonický rad je síce podmienečne konvergentný, ale nie je absolútne konvergentný: ak sa členy radu systematicky preskupia, súčet sa vo všeobecnosti zmení a v závislosti od preskupenia môže byť dokonca nekonečný.

Vzorec striedavého harmonického radu je špeciálnym prípadom Mercatorovho radu, Taylorovho radu pre prirodzený logaritmus.

Súvisiaci rad možno odvodiť z Taylorovho radu pre arktangens:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}. }

Tento postup je známy ako Leibnizov rad.

Všeobecné harmonické rady

Všeobecný harmonický rad má tvar

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}

kde a ≠ 0 a b sú reálne čísla a b/a nie je nula alebo záporné celé číslo.

Podľa testu limitného porovnania s harmonickým radom sa všetky všeobecné harmonické rady tiež rozchádzajú.

séria p

Zovšeobecnením harmonického radu je p-rad (alebo hyperharmonický rad), ktorý je definovaný ako

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

pre ľubovoľné reálne číslo p. Keď p = 1, p-rad je harmonický rad, ktorý sa rozchádza. Buď integrálny test, alebo Cauchyho kondenzačný test ukazuje, že p-rad konverguje pre všetky p > 1 (v takom prípade sa nazýva nadharmonický rad) a diverguje pre všetky p ≤ 1. Ak p > 1, potom súčet p-riadkov je ζ(p), t. j. Riemannova zeta funkcia vyhodnotená pri p.

Problém nájdenia súčtu pre p = 2 sa nazýva Bazilejský problém; Leonhard Euler ukázal, že je to π2/6. Hodnota súčtu pre p = 3 sa nazýva Apéryho konštanta, pretože Roger Apéry dokázal, že je to iracionálne číslo.

Séria ln

S radom p súvisí rad ln, ktorý je definovaný ako

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

pre ľubovoľné kladné reálne číslo p. Integrálnym testom sa dá dokázať, že pre p ≤ 1 diverguje, ale pre všetky p > 1 konverguje.

Séria φ

Pre každú konvexnú reálnu funkciu φ takú, že

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}}right)}{\varphi (u)}}<{\frac {1}{2}},}

seriál

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)}

je konvergentný. ^[]

Náhodné harmonické rady

Náhodný harmonický rad

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}

kde _sn sú nezávislé, identicky rozdelené náhodné premenné nadobúdajúce hodnoty +1 a -1 s rovnakou pravdepodobnosťou 1/2, je v teórii pravdepodobnosti známy príklad radu náhodných premenných, ktorý konverguje s pravdepodobnosťou 1. Skutočnosť tejto konvergencie je jednoduchým dôsledkom buď Kolmogorovovej vety o troch radoch, alebo úzko súvisiacej Kolmogorovovej maximálnej nerovnosti. Byron Schmuland z University of Alberta ďalej skúmal vlastnosti náhodného harmonického radu a ukázal, že konvergentný rad je náhodná veličina s niektorými zaujímavými vlastnosťami. Najmä funkcia hustoty pravdepodobnosti tejto náhodnej premennej vyhodnotená pri +2 alebo pri -2 nadobúda hodnotu 0,12499999999999999999999999999999764..., ktorá sa od 1/8 líši o menej ako 10-42. Schmulandov článok vysvetľuje, prečo je táto pravdepodobnosť tak blízko, ale nie presne 1/8. Presná hodnota tejto pravdepodobnosti je daná integrálom nekonečného kosínusového súčinu _C2 deleného π.

Vyčerpaný harmonický rad

Možno ukázať, že ochudobnený harmonický rad, v ktorom sú odstránené všetky členy, v ktorých sa kdekoľvek v menovateli vyskytuje číslica 9, konverguje a jeho hodnota je menšia ako 80. V skutočnosti, keď sa odstránia všetky členy obsahujúce akýkoľvek konkrétny reťazec číslic (v akomkoľvek základe), rad konverguje.

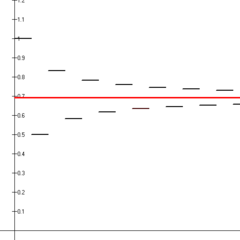
Prvých štrnásť čiastkových súčtov striedavých harmonických radov (čierne úsečky), ktoré konvergujú k prirodzenému logaritmu 2 (červená čiara).

Aplikácie

Harmonický rad môže byť kontraintuitívny. Je to preto, že ide o divergentný rad, hoci členy radu sa zmenšujú a smerujú k nule. Divergencia harmonického radu je zdrojom niektorých paradoxov.

• "Červ na gumičke". Predpokladajme, že po nekonečne pružnej metrovej gumičke sa plazí červík v rovnakom čase, ako je gumička rovnomerne natiahnutá. Ak sa červ pohybuje 1 centimeter za minútu a gumička sa naťahuje 1 meter za minútu, dosiahne červ niekedy koniec gumičky? Odpoveď je proti intuícii "áno", pretože po n minútach je pomer vzdialenosti, ktorú prejde červík, k celkovej dĺžke gumičky

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}. }

Keďže s rastúcim n sa rad ľubovoľne zväčšuje, nakoniec musí tento pomer presiahnuť 1, čo znamená, že červ dosiahne koniec gumičky. Hodnota n, pri ktorej k tomu dôjde, však musí byť extrémne veľká: približne e100, čo je číslo presahujúce 1043 minút (1037 rokov). Harmonický rad sa síce rozchádza, ale veľmi pomaly.

• Problém Jeepu sa pýta, koľko celkového paliva potrebuje auto s obmedzenou kapacitou na prejazd púšte, pričom na trase zostávajú kvapky paliva. Vzdialenosť, ktorú môže auto prejsť s daným množstvom paliva, súvisí s parciálnymi súčtami harmonických radov, ktoré rastú logaritmicky. A tak potrebné palivo rastie exponenciálne s požadovanou vzdialenosťou.

• Problém ukladania kociek na seba: ak je daná zbierka rovnakých kociek domina, je možné ich uložiť na okraj stola tak, aby viseli cez okraj stola bez toho, aby spadli. Protichodným výsledkom je, že ich možno poskladať tak, aby previs bol ľubovoľne veľký. Teda za predpokladu, že je dostatok kociek domina.

• Plavec, ktorý pri každom dotyku steny bazéna zrýchľuje. Plavec začína prekonávať desaťmetrový bazén rýchlosťou 2 m/s a s každým prekonaním sa mu pridajú ďalšie 2 m/s. Teoreticky je rýchlosť plavca neobmedzená, ale počet preplávaní bazéna potrebných na dosiahnutie tejto rýchlosti sa stáva veľmi veľkým; napríklad na dosiahnutie rýchlosti svetla (ignorujúc špeciálnu teóriu relativity) musí plavec preplávať bazén 150 miliónov krát. Na rozdiel od tohto veľkého čísla čas potrebný na dosiahnutie danej rýchlosti závisí od súčtu radov pri ľubovoľnom počte prekročení bazéna:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}. }

Výpočet súčtu ukazuje, že čas potrebný na dosiahnutie rýchlosti svetla je len 97 sekúnd.

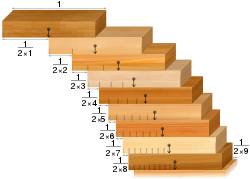
Problém ukladania blokov: bloky usporiadané podľa harmonického radu premosťujú štiepiny ľubovoľnej šírky.

Súvisiace stránky

• Harmonická progresia
• Zoznam súčtov reciprokých čísel