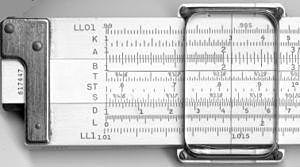
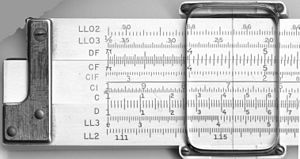
Logaritmické pravítko

Základné pojmy

Vo svojej najzákladnejšej podobe používa posuvné pravidlo dve logaritmické stupnice, ktoré umožňujú rýchle násobenie a delenie čísel. Tieto bežné operácie môžu byť časovo náročné a náchylné na chyby, ak sa vykonávajú na papieri. Zložitejšie posuvné pravidlá umožňujú ďalšie výpočty, napríklad odmocniny, exponenciály, logaritmy a trigonometrické funkcie.

Matematické výpočty sa vykonávajú vyrovnaním značky na posuvnom stredovom páse so značkou na jednom z pevných pásov. Potom sa môže sledovať relatívna poloha ostatných značiek. Čísla zarovnané so značkami udávajú približnú hodnotu súčinu, podielu alebo iného vypočítaného výsledku.

Používateľ určí polohu desatinnej čiarky vo výsledku na základe mentálneho odhadu. Pri formálnejších výpočtoch sa na sledovanie desatinnej čiarky používa vedecký zápis. Kroky sčítania a odčítania vo výpočte sa spravidla vykonávajú mentálne alebo na papieri, nie na posuvnom pravidle.

Väčšina posuvných pravidiel má tri lineárne pásy rovnakej dĺžky. Pásy sú rovnobežne usporiadané a vzájomne prepojené tak, aby sa stredný pás mohol pozdĺžne pohybovať vzhľadom na ostatné dva. Dva vonkajšie pásy sú pevné, takže ich vzájomná poloha sa nemení.

Niektoré posuvné pravidlá ("duplexné" modely) majú stupnice na oboch stranách pravidla a posuvnej lišty, iné na jednej strane vonkajších líšt a oboch stranách posuvnej lišty, ďalšie len na jednej strane ("simplexné" pravidlá). Posuvný kurzor so zvislou zarovnávacou čiarou sa používa na vyhľadávanie zodpovedajúcich bodov na stupniciach, ktoré nie sú vedľa seba alebo sa v prípade duplexných modelov nachádzajú na druhej strane pravidla. Kurzor môže zaznamenať aj medzivýsledok na ktorejkoľvek zo stupníc.

Kurzor na posuvnom meradle

Použitie posuvného pravidla na výpočet

Násobenie

Logaritmus transformuje operácie násobenia a delenia na sčítanie a odčítanie podľa pravidiel log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} a log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} . Posunutím hornej stupnice doprava o vzdialenosť log ( x ) {\displaystyle \log(x)} Porovnaním začiatku hornej stupnice s označením x {\displaystyle x} na spodnej strane sa každé číslo y {\displaystyle y} zarovná na pozícii log ( y ) {\displaystyle \log(y)} na hornej stupnici s číslom na pozícii log ( x ) + log ( y ) {\displaystyle \log(x)+\log(y)} na dolnej stupnici. Pretože log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+\log(y)=\log(xy)} Táto poloha na spodnej stupnici dáva x y {\displaystyle xy} , súčin x {\displaystyle x} a y {\displaystyle y} . Napríklad na výpočet 3*2 sa 1 na hornej stupnici presunie na 2 na dolnej stupnici. Odpoveď, 6, sa odčíta zo spodnej stupnice, kde je 3 na hornej stupnici. Vo všeobecnosti sa 1 na hornej stupnici presunie na faktor na dolnej stupnici a odpoveď sa odčíta z dolnej stupnice, kde je druhý faktor na hornej stupnici.

Operácie môžu ísť "mimo stupnice"; napríklad na obrázku vyššie je vidieť, že posuvné meradlo neumiestnilo číslo 7 na hornej stupnici nad žiadne číslo na dolnej stupnici, takže nedáva žiadnu odpoveď pre 2×7. V takýchto prípadoch môže používateľ posúvať hornú stupnicu doľava, až kým sa jej pravý index nevyrovná s číslom 2, čím sa účinne vynásobí číslom 0,2 namiesto číslom 2, ako je to znázornené na obrázku nižšie:

Tu musí používateľ posuvného meradla pamätať na to, aby vhodne upravil desatinnú čiarku a opravil tak konečnú odpoveď. Chceli sme nájsť 2×7, ale namiesto toho sme vypočítali 0,2×7=1,4. Takže skutočná odpoveď nie je 1,4, ale 14. Vynulovanie sklíčka nie je jediným spôsobom, ako riešiť násobenie, ktoré by viedlo k výsledkom mimo stupnice, ako napríklad 2×7; existujú aj iné metódy:

• (1) Použite dvojdekádové stupnice A a B.
• (2) Použite zložené váhy. V tomto príklade nastavte ľavú 1 z C oproti 2 z D. Presuňte kurzor na 7 na CF a výsledok prečítajte z DF.
• (3) Použite obrátenú stupnicu CI. Umiestnite 7 na stupnici CI nad 2 na stupnici D a potom odčítajte výsledok zo stupnice D pod 1 na stupnici CI. Keďže 1 sa na stupnici CI vyskytuje na dvoch miestach, jedno z nich bude vždy na stupnici.
• (4) Používajte inverznú stupnicu CI aj stupnicu C. Zarovnajte dvojku CI s jednotkou D a výsledok odčítajte z D pod číslicou 7 na stupnici C.

Metóda 1 je ľahko pochopiteľná, ale znamená stratu presnosti. Metóda 3 má tú výhodu, že zahŕňa len dve stupnice.

Divízia

Na obrázku nižšie je znázornený výpočet 5,5/2. Dvojka na hornej stupnici je umiestnená nad 5,5 na dolnej stupnici. Jednotka na hornej stupnici leží nad kvocientom 2,75. Existuje viacero spôsobov delenia, ale tu uvedený spôsob má tú výhodu, že konečný výsledok nemôže byť mimo stupnice, pretože človek má na výber, či použije 1 na oboch koncoch.

Ostatné operácie

Okrem logaritmických stupníc majú niektoré posuvné pravidlá zakódované aj ďalšie matematické funkcie na iných pomocných stupniciach. Najobľúbenejšie boli trigonometrické, zvyčajne sínus a tangens, obyčajný logaritmus (log10) (na prevzatie logaritmu hodnoty na stupnici násobenia), prirodzený logaritmus (ln) a exponenciálna stupnica (e^x). Niektoré pravidlá zahŕňajú Pytagorovu stupnicu na určovanie strán trojuholníkov a stupnicu na určovanie kružníc. Iné obsahujú stupnice na výpočet hyperbolických funkcií. V lineárnych pravidlách sú stupnice a ich označovanie veľmi štandardizované, pričom rozdiely sa zvyčajne vyskytujú len v tom, ktoré stupnice sú zahrnuté a v akom poradí:

A, B	logaritmické stupnice s dvoma dekadami, ktoré sa používajú na hľadanie odmocnín a štvorcov čísel
C, D	logaritmické stupnice na jednu dekádu
K	trojdielna logaritmická stupnica, ktorá sa používa na hľadanie kubických koreňov a kubických čísel
CF, DF	"zložené" verzie stupníc C a D, ktoré začínajú od π a nie od jednoty; sú vhodné v dvoch prípadoch. Po prvé, keď používateľ odhaduje, že súčin bude blízko 10, ale nie je si istý, či bude o niečo menší alebo o niečo väčší ako 10, zložené stupnice zabraňujú možnosti vybočenia zo stupnice. Po druhé, tým, že začiatok je π, a nie odmocnina z 10, násobenie alebo delenie π (ako je to bežné vo vedeckých a technických vzorcoch) sa zjednodušuje.
CI, DI, DIF	"obrátenú" stupnicu sprava doľava, ktorá sa používa na zjednodušenie krokov 1/x
S	používa sa na hľadanie sínusov a kosínusov na stupnici D
T	používa sa na hľadanie dotyčníc a kotangensov na stupniciach D a DI
ST, SRT	používa sa na sínusy a tangensy malých uhlov a prevod stupňov na radiány
L	lineárna stupnica, ktorá sa používa spolu so stupnicami C a D na hľadanie logaritmov so základom 10 a mocnín 10
LLn	súbor logaritmických stupníc, ktoré sa používajú na hľadanie logaritmov a exponenciálov čísel
Ln	lineárna stupnica, ktorá sa používa spolu so stupnicami C a D na hľadanie prirodzených logaritmov (základ e) a e x {\displaystyle e^{x}}

 

Stupnice na prednej a zadnej strane posuvného meradla K&E 4081-3.

Binárne posuvné pravidlo vyrobené spoločnosťou Gilson v roku 1931 vykonávalo funkciu sčítania a odčítania obmedzenú na zlomky.

Korene a právomoci

Existujú jednodekádové (C a D), dvojdekádové (A a B) a trojdekádové (K) stupnice. Na výpočet x {\displaystyle2 x^{2}} napríklad, nájdite x na stupnici D a odčítajte jeho štvorec na stupnici A. Obrátenie tohto postupu umožňuje nájsť odmocniny a podobne aj mocniny 3, 1/3, 2/3 a 3/2. Pozor si treba dať, keď sa základ x nachádza na viac ako jednom mieste svojej stupnice. Napríklad na stupnici A sú dve deviatky; ak chceme nájsť druhú odmocninu z deviatich, použijeme prvú, druhá dáva druhú odmocninu z 90.

Pre problémy x y {\displaystyle x^{y}} použite stupnice LL. Ak je prítomných niekoľko LL stupníc, použite tú, na ktorej je x. Najskôr zarovnajte krajnú ľavú 1 na stupnici C s x na stupnici LL. Potom nájdite y na stupnici C a prejdite na stupnicu LL, na ktorej je x. Táto stupnica bude označovať odpoveď. Ak je y "mimo stupnice", nájdite x y / {\displaystyle2 x^{y/2}} a vyrovnajte ho pomocou stupníc A a B, ako je opísané vyššie.

Trigonometria

Stupnice S, T a ST sa používajú pre trigonometrické funkcie a násobky trigonometrických funkcií, pre uhly v stupňoch. Mnohé posuvné pravidlá majú stupnice S, T a ST označené stupňami a minútami. Takzvané decitrigové modely používajú namiesto toho desatinné zlomky stupňov.

Logaritmy a exponenciály

Logaritmy a exponenciály základu 10 sa nachádzajú pomocou stupnice L, ktorá je lineárna. Niektoré posuvné pravidlá majú stupnicu Ln, ktorá je pre základ e.

Ln stupnicu vynašiel v roku 1958 žiak 11. ročníka Stephen B. Cohen. Pôvodným zámerom bolo umožniť používateľovi vybrať exponent x (v rozsahu 0 až 2,3) na stupnici Ln a odčítať e^x na stupnici C (alebo D) a e ^–xna stupnici CI (alebo DI). Výhradné práva na stupnicu získala spoločnosť Pickett, Inc. Neskôr vynálezca vytvoril súbor "značiek" na stupnici Ln na rozšírenie rozsahu za hranicu 2,3, ale spoločnosť Pickett tieto značky nikdy nezaviedla na žiadne zo svojich posuvných pravidiel. ^[]

Sčítanie a odčítanie

Posuvné pravidlá sa zvyčajne nepoužívajú na sčítanie a odčítanie, ale napriek tomu je to možné pomocou dvoch rôznych techník.

Prvá metóda na vykonanie sčítania a odčítania na stupni C a D (alebo na akejkoľvek porovnateľnej stupnici) vyžaduje premenu problému na delenie. Pri sčítaní sa kvocient dvoch premenných plus jeden krát deliteľ rovná ich súčtu:

x + y = ( x y + ) 1y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}

Pri odčítaní sa podiel dvoch premenných mínus jedna krát deliteľ rovná ich rozdielu:

x - y = ( x y -1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y}

Táto metóda je podobná technike sčítania/odčítania používanej pri vysokorýchlostných elektronických obvodoch s logaritmickou číselnou sústavou v špecializovaných počítačových aplikáciách, ako je superpočítač GRAPE (Gravity Pipe) a skryté Markovove modely.

Druhá metóda využíva posuvnú lineárnu stupnicu L, ktorá je k dispozícii v niektorých modeloch. Sčítanie a odčítanie sa vykonáva posunutím kurzora doľava (pre odčítanie) alebo doprava (pre sčítanie) a následným vrátením posuvníka na hodnotu 0, čím sa prečíta výsledok.

Fyzický dizajn

Štandardné lineárne pravidlá

Dĺžka posuvného meradla sa udáva ako menovitá dĺžka stupníc. Stupnice na najbežnejších "10-palcových" modeloch majú v skutočnosti dĺžku 25 cm, pretože boli vyrobené podľa metrických noriem, hoci niektoré pravidlá ponúkajú mierne predĺžené stupnice na zjednodušenie manipulácie pri pretečení výsledku. Vreckové pravidlá majú zvyčajne 5 palcov. Predávali sa modely dlhé niekoľko metrov, ktoré sa zavesili do učební na vyučovacie účely. [1]

Obvykle sa na stupnici vyznačí delenie s presnosťou na dve platné čísla a používateľ odhadne tretie číslo. Niektoré špičkové posuvné pravidlá majú zväčšovacie kurzory, ktoré uľahčujú viditeľnosť značiek. Takéto kurzory môžu účinne zdvojnásobiť presnosť čítania, čo umožňuje, aby 10-palcové posuvné meradlo slúžilo rovnako dobre ako 20-palcové.

Boli vyvinuté rôzne ďalšie vymoženosti. Trigonometrické stupnice sú niekedy označené dvojitým štítkom, čiernou a červenou farbou, s doplnkovými uhlami, takzvaným "darmstadtským" štýlom. Obojstranné posuvné pravidlá často duplikujú niektoré stupnice na zadnej strane. Stupnice sú často "rozdelené", aby sa dosiahla vyššia presnosť.

Špecializované posuvné pravidlá boli vynájdené pre rôzne formy inžinierstva, obchodu a bankovníctva. Často mali bežné výpočty priamo vyjadrené ako špeciálne stupnice, napríklad výpočty pôžičiek, optimálne nákupné množstvá alebo konkrétne technické rovnice. Napríklad spoločnosť Fisher Controls distribuovala prispôsobené posuvné pravidlo prispôsobené na riešenie rovníc používaných na výber správnej veľkosti priemyselných regulačných ventilov prietoku. ^[]

Kruhové posuvné pravidlá

Kruhové posuvné pravítka sa vyrábajú v dvoch základných typoch: s dvoma kurzormi (vľavo) a s pohyblivým kotúčom a jedným kurzorom (vpravo). Verzie s dvoma kurzormi vykonávajú násobenie a delenie udržiavaním pevného uhla medzi kurzormi pri ich otáčaní okolo kotúča. Verzia s jedným kurzorom funguje skôr ako štandardné posuvné meradlo vďaka vhodnému nastaveniu stupníc.

Základnou výhodou kruhového posuvného meradla je, že najdlhší rozmer nástroja sa zmenšil približne 3-krát (t. j. o π). Napríklad vonkajšia stupnica 10 cm kruhového pravítka by mala maximálnu presnosť rovnajúcu sa 30 cm bežného posuvného pravítka. Kruhové posuvné pravidlá tiež eliminujú výpočty "mimo stupnice", pretože stupnice boli navrhnuté tak, aby "obopínali"; nikdy sa nemusia preorientovávať, keď sa výsledky blížia k 1,0 - pravidlo je vždy na stupnici. Pri necyklických nespirálových stupniciach, ako sú S, T a LL, sa však dĺžka stupnice skracuje, aby sa vytvoril priestor pre koncové okraje.

Kruhové posuvné meradlá sú mechanicky robustnejšie a hladšie sa pohybujú, ale ich presnosť nastavenia stupnice je citlivá na vycentrovanie centrálneho čapu; nepatrné odchýlenie čapu o 0,1 mm môže mať v najhoršom prípade za následok chybu nastavenia 0,2 mm. Čap však zabraňuje poškriabaniu čelnej plochy a kurzorov. Stupnice s najvyššou presnosťou sú umiestnené na vonkajších krúžkoch. Namiesto "delených" stupníc používajú špičkové kruhové pravidlá špirálové stupnice na zložitejšie operácie, ako sú logaritmické stupnice. Jedno osempalcové prémiové kruhové pravidlo malo 50-palcovú špirálovú logaritmickú stupnicu.

Hlavnými nevýhodami kruhových posuvných pravidiel sú ťažkosti pri umiestňovaní číslic pozdĺž rotujúceho kotúča a obmedzený počet stupníc. Ďalšou nevýhodou kruhových posuvných pravidiel je, že menej dôležité stupnice sú bližšie k stredu a majú nižšiu presnosť. Väčšina študentov sa naučila používať posuvné pravidlá na lineárnych posuvných pravidlách a nenašla dôvod na zmenu.

Jedným z posuvných meradiel, ktoré sa stále používajú na celom svete, je E6B. Ide o kruhové posuvné pravidlo, ktoré bolo prvýkrát vytvorené v 30. rokoch 20. storočia pre pilotov lietadiel na pomoc pri mŕtvom ťahu. Pomocou stupníc vytlačených na ráme pomáha aj pri rôznych úlohách, ako je prepočet času, vzdialenosti, rýchlosti a teploty, chyby kompasu a výpočet spotreby paliva. Takzvané "modlitebné koliesko" je stále k dispozícii v leteckých predajniach a naďalej sa hojne používa. Hoci GPS obmedzil používanie mŕtveho ťahu na leteckú navigáciu a mnohé jeho funkcie prevzali ručné kalkulačky, E6B sa naďalej široko používa ako primárny alebo záložný prístroj a väčšina leteckých škôl vyžaduje, aby ich študenti ovládali tento prístroj do určitej miery.

V roku 1952 predstavila švajčiarska hodinárska spoločnosť Breitling náramkové hodinky pre pilotov s integrovaným kruhovým posuvným pravidlom špecializovaným na letové výpočty: Breitling Navitimer. Kruhové pravidlo Navitimer, ktoré spoločnosť Breitling označovala ako "navigačný počítač", obsahovalo funkcie určovania rýchlosti letu, rýchlosti/času stúpania/klesania, času letu, vzdialenosti a spotreby paliva, ako aj funkcie prepočtu kilometrov na námorné míle a množstva paliva v galónoch na litre.

Materiály

Tradične sa posuvné pravidlá vyrábali z tvrdého dreva, ako je mahagón alebo borovica, s kurzormi zo skla a kovu. Najmenej jeden veľmi presný nástroj bol vyrobený z ocele.

V roku 1895 začala japonská firma Hemmi vyrábať posuvné pravidlá z bambusu, ktorého výhodou bola rozmerová stabilita, pevnosť a prirodzené samomazanie. Tieto bambusové posuvné pravidlá boli uvedené na trh vo Švédsku v septembri 1933 [2] a pravdepodobne len o niečo skôr v Nemecku. Stupnice boli vyrobené z celuloidu alebo plastu. Neskôr sa posuvné pravidlá vyrábali z plastu alebo z hliníka natretého plastom. Neskoršie kurzory boli akrylátové alebo polykarbonátové, ktoré sa posúvali na teflónových ložiskách.

Všetky prémiové posuvné pravidlá mali vyryté čísla a stupnice a potom boli vyplnené farbou alebo inou živicou. Maľované alebo potlačené posuvné pravidlá sa považovali za horšie, pretože značky sa mohli opotrebovať. Napriek tomu spoločnosť Pickett, pravdepodobne najúspešnejšia americká spoločnosť vyrábajúca posuvné pravidlá, vyrábala všetky tlačené stupnice. Prémiové posuvné pravidlá obsahovali dômyselné západky, aby sa pravidlo náhodou nerozpadlo, a nárazníky, ktoré chránili stupnice a kurzor pred trením o stolovú dosku. Odporúčaná metóda čistenia vyrytých značiek je ľahké drhnutie oceľovou vlnou. Na maľované posuvné pravidlá a pre slabé povahy použite zriedenú komerčnú kvapalinu na čistenie okien a mäkkú handričku.

Pickettovo kruhové posuvné meradlo s dvoma kurzormi. (priemer 4,25 palca / 10,9 cm) Zadná strana má ďalšiu stupnicu a jeden kurzor.


Jednoduché kruhové posuvné meradlo, vyrobené spoločnosťou Concise Co., Ltd., Tokio, Japonsko, len s inverznou, štvorcovou a kubickou stupnicou. Na zadnej strane je praktický zoznam 38 metrických/imperiálnych prevodových faktorov.


Náramkové hodinky Breitling Navitimer s kruhovým posuvným meradlom

História

Pravidlo bolo vynájdené v rokoch 1620-1630, krátko po tom, čo John Napier uverejnil koncept logaritmu. Edmund Gunter z Oxfordu vyvinul počítacie zariadenie s jednou logaritmickou stupnicou, ktoré sa s ďalšími meracími nástrojmi dalo použiť na násobenie a delenie. Prvý opis tejto stupnice uverejnil v Paríži v roku 1624 anglický matematik Edmund Wingate (asi 1593 - 1656) v knihe s názvom "L'usage de la reigle de proportion en l'arithmetique & geometrie". Kniha obsahuje dvojitú stupnicu, na ktorej jednej strane je logaritmická stupnica a na druhej strane tabuľková stupnica. V roku 1630 William Oughtred z Cambridge vynašiel kruhové posuvné pravidlo a v roku 1632 spojil dve Gunterove pravidlá, ktoré držal rukami, a vytvoril tak zariadenie, ktoré je rozpoznateľné ako moderné posuvné pravidlo. Podobne ako jeho súčasník v Cambridgei Isaac Newton, aj Oughtred vyučoval svoje myšlienky súkromne svojim študentom, ale otáľal s ich publikovaním a podobne ako Newton sa zapojil do vášnivého sporu o prioritu so svojím niekdajším študentom Richardom Delamainom a predchádzajúcimi nárokmi Wingatea. Oughtredove myšlienky boli zverejnené až v publikáciách jeho študenta Williama Forstera v rokoch 1632 a 1653.

V roku 1677 Henry Coggeshall vytvoril dvojstopové skladacie pravidlo na meranie dreva, nazývané Coggeshallovo posuvné pravidlo. Jeho konštrukcia a použitie tohto nástroja dali posuvnému pravidlu účel aj mimo matematického skúmania.

V roku 1722 Warner zaviedol dvoj- a trojdielnu stupnicu a v roku 1755 Everard zaradil inverznú stupnicu; posuvné pravidlo obsahujúce všetky tieto stupnice sa zvyčajne označuje ako "viacfázové" pravidlo.

V roku 1815 vynašiel Peter Roget posuvné pravidlo logaritmu, ktoré obsahovalo stupnicu zobrazujúcu logaritmus logaritmu. To umožnilo používateľovi priamo vykonávať výpočty zahŕňajúce odmocniny a exponenty. Bolo to užitočné najmä pre zlomkové mocniny.

Moderná forma

Modernejšiu formu vytvoril v roku 1859 francúzsky delostrelecký poručík Amédée Mannheim, "ktorý mal šťastie, že jeho pravidlo vyrobila firma s národnou reputáciou a že ho prijalo francúzske delostrelectvo". Približne v tom čase, keď sa inžinierstvo stalo uznávanou profesionálnou činnosťou, sa v Európe začali používať posuvné pravidlá. V Spojených štátoch sa rozšírili až v roku 1881, keď tam Edwin Thacher predstavil valcové pravidlo. Obojstranné pravidlo vynašiel William Cox v roku 1891 a vyrábala ho spoločnosť Keuffel and Esser Co. z New Yorku.

Astronomická práca si vyžadovala aj presné výpočty a v 19. storočí sa v jednom observatóriu v Nemecku používalo oceľové posuvné pravidlo dlhé asi 2 metre. Bolo pripojené k mikroskopu, čo mu umožňovalo presnosť na šesť desatinných miest.

V druhej svetovej vojne bombardéri a navigátori, ktorí potrebovali rýchle výpočty, často používali špecializované posuvné pravidlá. Jeden úrad amerického námorníctva skutočne navrhol všeobecné "šasi" posuvného pravidla s hliníkovým telom a plastovým kurzorom, do ktorého sa dali vložiť celuloidové karty (s obojstrannou potlačou) na špeciálne výpočty. Tento postup bol vynájdený na výpočet doletu, spotreby paliva a nadmorskej výšky lietadiel a potom prispôsobený na mnohé iné účely.

V 50. a 60. rokoch 20. storočia bolo posuvné meradlo symbolom povolania inžiniera (podobne ako stetoskop symbolizuje povolanie lekára).^[] Nemecký raketový vedec Wernher von Braun si po druhej svetovej vojne, keď sa presťahoval do USA, aby pracoval na americkom vesmírnom programe, priniesol so sebou dve historické posuvné pravidlá Nestler z 30. rokov. Počas svojho života nikdy nepoužíval žiadne iné vreckové počítacie zariadenia; posuvné pravidlá mu dokonale slúžili na rýchle odhady parametrov konštrukcie rakiet a iných údajov. Hliníkové posuvné pravidlá značky Pickett boli podľa reklamy na krabičkách s posuvnými pravidlami Pickett N600 [3] prepravované na piatich vesmírnych misiách Apollo vrátane letu na Mesiac.

Niektorí študenti techniky a inžinieri nosili desaťpalcové posuvné pravidlá v puzdrách na opasku a ešte v polovici 70. rokov 20. storočia to bolo na univerzitách bežné. Študenti si tiež mohli ponechať desať- alebo dvadsaťpalcové pravítko na presnú prácu doma alebo v kancelárii a zároveň so sebou nosiť päťpalcové vreckové posuvné meradlo.

V roku 2004 výskumníci v oblasti vzdelávania David B. Sher a Dean C. Nataro navrhli nový typ posuvného pravidla založeného na prostatafereze, algoritme na rýchle počítanie súčinov, ktorý vznikol ešte pred logaritmami. Praktický záujem o jeho zostrojenie však bol okrem pôvodného prototypu len malý. [4]

Pokles

Význam posuvného meradla začal klesať, keď sa v 60. rokoch 20. storočia stali pre technických pracovníkov široko dostupnými elektronické počítače, ktoré boli v 50. rokoch 20. storočia novým, ale veľmi vzácnym zdrojom. Zavedením jazyka Fortran v roku 1957 sa počítače stali praktickými na riešenie skromných matematických problémov. IBM uviedla sériu cenovo dostupnejších počítačov IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965) určených pre vedecký a technický trh. Programovací jazyk BASIC Johna Kemenyho (1964) uľahčil študentom používanie počítačov. V roku 1965 bol predstavený minipočítač DEC PDP-8.

Počítače zmenili aj povahu výpočtov. Pri posuvných pravidlách sa kládol veľký dôraz na prácu s algebrou, aby sa výrazy dostali do čo najlepšie vypočítateľnej podoby. Používatelia posuvných pravidiel jednoducho aproximovali alebo vypúšťali malé výrazy, aby zjednodušili výpočet. Fortran umožnil zadávať komplikované vzorce z učebníc bez námahy s preformulovaním. Numerická integrácia bola často jednoduchšia ako hľadanie riešení zložitých problémov v uzavretom tvare. Mladý inžinier žiadajúci počítačový čas na vyriešenie problému, ktorý sa dal vyriešiť niekoľkými ťahmi na posuvnom pravidle, sa stal humorným klišé. Mnohé počítačové centrá mali na stene zavesené zarámované posuvné pravidlo s poznámkou "V prípade núdze rozbiť sklo".

Ďalším krokom k nahradeniu posuvných pravidiel elektronikou bol vývoj elektronických kalkulačiek na vedecké a technické účely. Medzi prvé patrili LOCI-2 od spoločnosti Wang Laboratories, uvedený na trh v roku 1965, ktorý používal logaritmy na násobenie a delenie, a HP-9100 od spoločnosti Hewlett-Packard, uvedený na trh v roku 1968. Model HP-9100 mal okrem exponenciál a logaritmov aj trigonometrické funkcie (sin, cos, tan). Používal algoritmus CORDIC (coordinate rotation digital computer), ktorý umožňuje výpočet trigonometrických funkcií len pomocou operácií posunu a sčítania. Táto metóda uľahčila vývoj stále menších vedeckých kalkulačiek.

Posledným klincom do rakvy posuvného pravidla bolo uvedenie vreckových vedeckých kalkulačiek, z ktorých prvou bola v roku 1972 kalkulačka Hewlett-Packard HP-35. Takéto kalkulačky sa začali označovať ako "slide rule" kalkulačky, pretože mohli vykonávať väčšinu alebo všetky funkcie slide rule. Aj tieto kalkulačky za niekoľko stoviek dolárov boli pre väčšinu študentov považované za drahé. Hoci profesionálne posuvné kalkulačky mohli byť aj pomerne drahé, v drogériách sa často predávali základné plastové modely za menej ako 20 USD. V roku 1975 sa však základné štvorfunkčné elektronické kalkulačky dali kúpiť za menej ako 50 USD. V roku 1976 ponúkal TI-30 vedeckú kalkulačku za menej ako 25 USD. Po tomto období trh s posuvnými pravidlami rýchlo vyschol, pretože malé vedecké kalkulačky sa stali cenovo dostupnými.

William Oughtred (1575-1660), vynálezca kruhového posuvného meradla


Inžinier používa posuvné meradlo. Všimnite si mechanickú kalkulačku v pozadí.


TI-30

Výhody

• Posuvné pravidlo má tendenciu zmierňovať omyl "falošnej presnosti" a významnosti. Typická presnosť, ktorú má používateľ posuvného pravidla k dispozícii, je približne tri miesta presnosti. To dobre korešponduje s väčšinou údajov, ktoré sú k dispozícii na vstup do technických vzorcov. Pri použití modernej vreckovej kalkulačky sa presnosť môže zobrazovať na sedem alebo viac desatinných miest, pričom v skutočnosti výsledky nikdy nemôžu mať väčšiu presnosť, ako sú dostupné vstupné údaje.
• Posuvné pravidlo si vyžaduje priebežný odhad poradia veľkosti výsledkov. Na posuvnom pravidle 1,5 × 30 (čo sa rovná 45) sa zobrazí rovnaký výsledok ako 1 500 000 × 0,03 (čo sa rovná 45 000). Je na inžinierovi, aby neustále určoval primeranosť výsledkov, čo sa môže stratiť pri nedbalom zadávaní čísel do počítačového programu alebo kalkulačky.
• Pri postupnom násobení alebo delení tým istým číslom možno odpoveď často určiť len pohľadom na posuvné meradlo bez akejkoľvek manipulácie. To môže byť užitočné najmä pri výpočte percent, napr. pri výsledkoch testov, alebo pri porovnávaní cien, napr. v dolároch za kilogram. Viaceré výpočty rýchlosti, času a vzdialenosti možno pomocou posuvného meradla vykonať bez použitia rúk a jedným pohľadom.
• Pravítko nie je závislé od elektriny.
• Pravítko je ľahko replikovateľná technológia. Z daného príkladu posuvného pravidla môže schopný remeselník zostrojiť ďalšie zo základných materiálov s použitím nepriemyselných postupov.
• Posuvné pravidlá sú vysoko štandardizované, takže pri prechode na iné pravidlo sa nemusíte nič učiť odznova.
• Posuvné pravidlá sú všestranné a možno ich používať v situáciách a prostrediach, v ktorých môže mať používateľ zníženú obratnosť (napríklad z dôvodu potreby ochranných rukavíc). Naopak, kalkulačku možno v takýchto situáciách ťažko ovládať - pri použití posuvného pravidla je nepravdepodobné, že by došlo k podobnej chybe ako pri chybnom stlačení nesprávneho tlačidla na kalkulačke.
• Posuvné pravidlá môžu byť vyrobené z kartónu alebo papiera. Mnohé voľné tabuľky alebo špecializované počítacie zariadenia vyrobené z kartónu sú vlastne špecializované lineárne alebo kruhové posuvné pravidlá.

Jednou z výhod používania posuvného pravidla spolu s elektronickou kalkulačkou je, že dôležitý výpočet možno skontrolovať na oboch prístrojoch; pretože oba prístroje sú veľmi odlišné, je malá pravdepodobnosť, že urobíte rovnakú chybu dvakrát.

Nevýhody

• Chyby môžu vzniknúť mechanickou nepresnosťou.
• Výpočty pomocou posuvného meradla majú obmedzenú presnosť kvôli ich analógovým vstupom a výstupom. Naopak, kvôli diskrétnym číselným vstupom a elektronickým operáciám s pohyblivou rádovou čiarkou majú aj skromné moderné kalkulačky výstupné rozlíšenie aspoň šesť významných čísel.

Súvisiace stránky

• Abacus
• Logaritmus