Algebra (disciplína)

História

Rané formy algebry vyvinuli Babylončania a grécki geometri, ako napríklad Hérós Alexandrijský. Slovo "algebra" je však latinská forma arabského slova Al-Jabr ("liatie") a pochádza z matematickej knihy Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Esej o výpočte liatia a rovnice"), ktorú v 9. storočí napísal perzský matematik Muhammad ibn Mūsā al-Khwārizmī, moslim narodený v Chvarizme v Uzbekistane. V rokoch 813 - 833 n. l. prekvital pod vedením Al-Ma'mouna v irackom Bagdade a zomrel okolo roku 840 n. l. Kniha sa dostala do Európy a v 12. storočí bola preložená do latinčiny. Kniha potom dostala názov "Algebra". (Koncovka matematikovho mena al-Khwarizmi sa zmenila na slovo, ktoré sa ľahšie vyslovuje v latinčine, a stalo sa z neho anglické slovo algorithm).

Príklady

Tu je jednoduchý príklad algebrického problému:

Sue má 12 cukríkov a Ann má 24 cukríkov. Rozhodnú sa, že sa podelia, aby mali rovnaký počet cukríkov. Koľko cukríkov bude mať každá z nich?

Toto sú kroky, ktoré môžete použiť na vyriešenie problému:

1. Aby mala rovnaký počet cukríkov, musí Ann dať nejaké Sue. Nech x predstavuje počet cukríkov, ktoré Ann dá Sue.
2. Sueine cukríky plus x musia byť rovnaké ako Annine cukríky mínus x: 12 + x = 24 - x
3. Od oboch strán rovnice odpočítajte 12. Vznikne: x = 12 - x. (To, čo sa deje na jednej strane znamienka rovnosti, sa musí diať aj na druhej strane, aby rovnica stále platila. Takže v tomto prípade, keď sa od oboch strán odčítalo 12, došlo k prostrednému kroku 12 + x - 12 = 24 - x - 12. Po tom, ako sa s tým človek vyrovná, sa stredný krok nezapisuje).
4. Pridajte x k obom stranám rovnice. Takto dostaneme: 2x = 12
5. Obe strany rovnice vydeľte číslom 2. Dostanete x = 6. Odpoveď je šesť. Ak Ann dá Sue 6 cukríkov, budú mať rovnaký počet cukríkov.
6. Ak si to chcete overiť, vložte 6 späť do pôvodnej rovnice, kde bolo x: 12 + 6 = 24 - 6
7. To dáva 18=18, čo je pravda. Každý z nich má teraz 18 cukríkov.

S praxou možno algebru použiť, keď sa stretnete s problémom, ktorý je príliš ťažký na to, aby ste ho vyriešili iným spôsobom. Problémy ako stavba diaľnice, návrh mobilného telefónu alebo hľadanie lieku na chorobu si vyžadujú algebru.

Písanie algebry

Tak ako vo väčšine matematiky, sčítanie z s y (alebo y plus z) sa zapisuje ako y + z. Odčítanie z od y (alebo y mínus z) sa zapisuje ako y - z. Delenie y z (alebo y nad z: y z {\displaystyle y \nad z} ) sa zapisuje ako y ÷ z alebo y/z. častejšie sa používa y/z.

V algebre sa násobenie y číslom z (alebo y krát z) môže zapísať 4 spôsobmi: y × z, y * z, y-z alebo len yz. Symbol násobenia "×" sa zvyčajne nepoužíva, pretože príliš pripomína písmeno x, ktoré sa často používa ako premenná. Aj pri násobení väčšieho výrazu sa môžu použiť zátvorky: y (z+1).

Keď v algebre násobíme číslo a písmeno, pred písmeno napíšeme číslo: 5 × y = 5y. Keď je číslo 1, tak 1 nepíšeme, pretože 1 krát ľubovoľné číslo je toto číslo (1 × y = y), a preto ho nepotrebujeme.

Poznámka na okraj: v algebre nemusíte používať písmená x alebo y. Premenné sú len symboly, ktoré znamenajú nejaké neznáme číslo alebo hodnotu, takže môžete použiť akúkoľvek premennú. x a y sú však najčastejšie.

Funkcie a grafy

Dôležitou súčasťou algebry je štúdium funkcií, pretože funkcie sa často objavujú v rovniciach, ktoré sa snažíme vyriešiť. Funkcia je ako stroj, do ktorého môžete vložiť číslo (alebo čísla) a dostať z neho určité číslo (alebo čísla). Pri používaní funkcií môžu byť grafy mocným nástrojom, ktorý nám pomôže pri štúdiu riešení rovníc.

Graf je obrázok, na ktorom sú znázornené všetky hodnoty premenných, vďaka ktorým je rovnica alebo nerovnica pravdivá. Zvyčajne sa dá ľahko vytvoriť, ak ide len o jednu alebo dve premenné. Grafom je často priamka, a ak sa priamka neohýba alebo nejde rovno hore-dole, možno ju opísať základným vzorcom y = mx + b. Premenná b je y-priesečník grafu (miesto, kde priamka pretína zvislú os) a m je sklon alebo strmosť priamky. Tento vzorec platí pre súradnice grafu, kde sa každý bod na priamke zapisuje (x, y).

V niektorých matematických úlohách, ako je napríklad rovnica priamky, môže byť viac ako jedna premenná (v tomto prípade x a y). Ak chcete nájsť body na priamke, jedna premenná sa zmení. Premenná, ktorá sa mení, sa nazýva "nezávislá" premenná. Potom sa vykonajú matematické výpočty, aby sa vytvorilo číslo. Číslo, ktoré sa vytvorí, sa nazýva "závislá" premenná. Väčšinou sa nezávislá premenná zapisuje ako x a závislá premenná ako y, napríklad v prípade y = 3x + 1. Často sa to znázorňuje do grafu pomocou osi x (smerujúcej doľava a doprava) a osi y (smerujúcej nahor a nadol). Môže sa zapísať aj vo forme funkcie: f(x) = 3x + 1. V tomto príklade by sme teda mohli za x dosadiť 5 a dostať y = 16. Ak by sme za x dosadili 2, dostali by sme y = 7. A 0 za x by sme dostali y=1. Takže bodmi (5,16), (2,7) a (0,1) by prechádzala priamka, ako je vidieť na grafe vpravo.

Ak má x mocninu 1, je to priamka. Ak je štvorcová alebo má inú mocninu, je zakrivená. Ak používa nerovnosť (< alebo > ), potom je zvyčajne časť grafu zatienená, buď nad alebo pod priamkou.

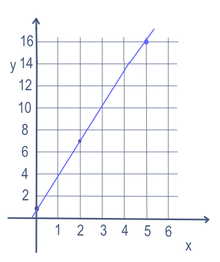
Lineárna rovnica pre y=3x+1

Pravidlá algebry

V algebre existuje niekoľko pravidiel, ktoré sa dajú použiť na ďalšie pochopenie rovníc. Tieto pravidlá sa nazývajú pravidlá algebry. Hoci sa tieto pravidlá môžu zdať nezmyselné alebo samozrejmé, je múdre si uvedomiť, že tieto vlastnosti neplatia vo všetkých odvetviach matematiky. Preto bude užitočné vedieť, ako sú tieto axiomatické pravidlá deklarované, skôr než ich budeme považovať za samozrejmé. Skôr ako prejdeme k pravidlám, zamyslime sa nad dvoma definíciami, ktoré budú uvedené.

1. Opak - opakom {\displaystyle a} je - a {\displaystyle -a}.
2. Vzájomná hodnota - vzájomná hodnota a {\displaystyle a} je 1 a {\displaystyle {\frac {1}{a}}} .

Pravidlá

Komutatívna vlastnosť sčítania

"Komutatívny" znamená, že funkcia má rovnaký výsledok, ak sa čísla zamenia. Inými slovami, na poradí členov v rovnici nezáleží. Ak je operátorom dvoch členov sčítanie, platí "komutatívna vlastnosť sčítania". V algebraickom vyjadrení to znamená, že a + b = b + a {\displaystyle a+b=b+a} .

Všimnite si, že to neplatí pre odčítanie! (t. j. a - b ≠ b - a {\displaystyle a-b\neq b-a} )

Komutatívna vlastnosť násobenia

Ak je operátorom dvoch členov násobenie, platí "komutatívna vlastnosť násobenia". V algebraickom vyjadrení to znamená a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} .

Upozorňujeme, že to neplatí pre delenie! (t.j. a b ≠ b a {\displaystyle {\frac {a}{b}}}neq {\frac {b}{a}}}} keď a ≠ b {\displaystyle a\neq b} )

Asociatívna vlastnosť sčítania

"Asociatívny" sa vzťahuje na zoskupenie čísel. Asociatívna vlastnosť sčítania znamená, že pri sčítaní troch alebo viacerých členov nezáleží na tom, ako sú tieto členy zoskupené. Algebraicky to znamená a + ( b + c ) = ( a + b ) + c {\displayystyle a+(b+c)=(a+b)+c} . Všimnite si, že toto neplatí pre odčítanie, napr. 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} (pozri distribučnú vlastnosť).

Asociatívna vlastnosť násobenia

Asociatívna vlastnosť násobenia znamená, že pri násobení troch alebo viacerých členov nezáleží na tom, ako sú tieto členy zoskupené. Algebraicky to dáva a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} . Všimnite si, že to neplatí pre delenie, napr. 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} .

Distributívna vlastnosť

Distributívna vlastnosť hovorí, že násobenie čísla iným členom možno rozložiť. Napríklad: a ⋅ ( b + c ) = a b + a c {\displayystyle a\cdot (b+c)=ab+ac} . (Nezamieňajte si to s asociatívnymi vlastnosťami! Napríklad a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} .)

Vlastnosť aditívnej identity

"Identita" označuje vlastnosť čísla, že sa rovná samému sebe. Inými slovami, existuje operácia dvoch čísel tak, že sa rovná premennej súčtu. Vlastnosť aditívnej identity hovorí, že súčet ľubovoľného čísla a 0 je toto číslo: a + 0 = a {\displayystyle a+0=a} . To platí aj pre odčítanie: a - 0 = a {\displaystyle a-0=a} .

Vlastnosť multiplikatívnej identity

Vlastnosť multiplikatívnej identity hovorí, že súčinom ľubovoľného čísla a 1 je toto číslo: a ⋅ 1 = a {\displaystyle a\cdot 1=a} . To platí aj pre delenie: a 1 = a {\displaystyle {\frac {a}{1}}=a} .

Aditívna inverzná vlastnosť

Aditívna inverzná vlastnosť je niečo ako opak aditívnej vlastnosti identity. Ak je operácia súčtom čísla a jeho opaku a rovná sa 0, je táto operácia platnou algebraickou operáciou. Algebraicky to znamená, že a - a = 0 {\displaystyle a-a=0} . Aditívna inverzná hodnota 1 je (-1).

Multiplikatívna inverzná vlastnosť

Multiplikatívna inverzná vlastnosť znamená, že ak je operácia súčinom čísla a jeho reciprokej hodnoty a rovná sa 1, je táto operácia platnou algebraickou operáciou. Algebraicky to znamená: a a = 1 {\displaystyle {\frac {a}{a}}=1} . Multiplikatívna inverzná hodnota 2 je 1/2.

Pokročilá algebra

Okrem "elementárnej algebry" alebo základnej algebry existujú aj pokročilé formy algebry, ktoré sa vyučujú na vysokých školách a univerzitách, ako napríklad abstraktná algebra, lineárna algebra a univerzálna algebra. Patrí sem aj to, ako používať maticu na riešenie mnohých lineárnych rovníc naraz. Abstraktná algebra je štúdium vecí, ktoré sa nachádzajú v rovniciach, pričom presahuje čísla a je abstraktnejšia pomocou skupín čísel.

Mnohé matematické úlohy sa týkajú fyziky a techniky. V mnohých z týchto fyzikálnych úloh je čas premennou. Čas používa písmeno t. Použitie základných myšlienok v algebre môže pomôcť zredukovať matematický problém na najjednoduchšiu formu, čo uľahčuje riešenie zložitých problémov. Energia je e, sila je f, hmotnosť je m, zrýchlenie je a a rýchlosť svetla je niekedy c. Toto sa používa v niektorých známych rovniciach, ako napríklad f = ma a e=mc^2 (hoci na vymyslenie poslednej rovnice bola potrebná zložitejšia matematika nad rámec algebry).

Súvisiace stránky

• Zoznam tém z matematiky
• Poradie operácií
• Parabola
• Systém počítačovej algebry